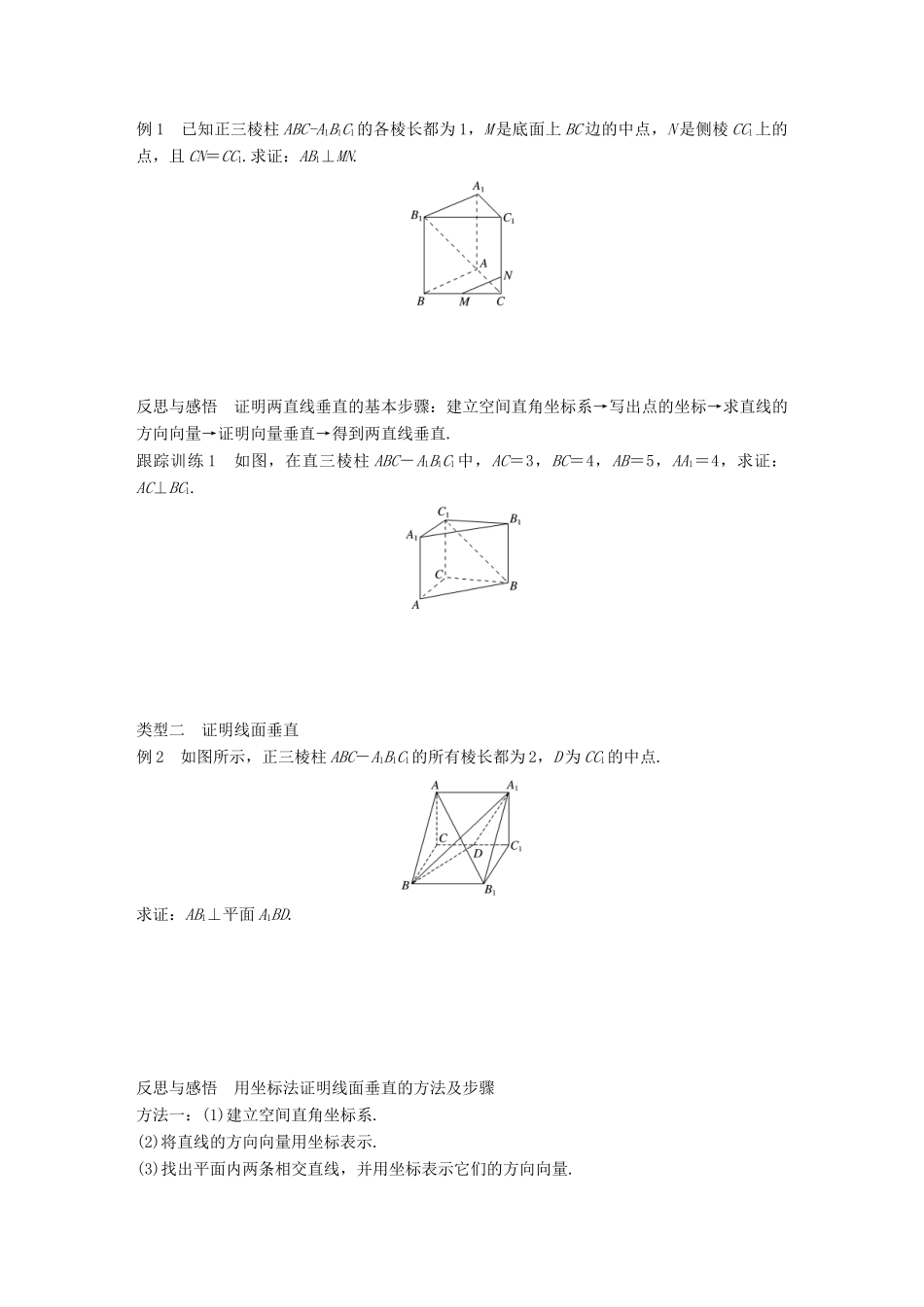
3.2.2 空间线面关系的判定(二)学习目标 1.能用向量法判断一些简单的线线、线面、面面垂直关系.2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.3.能用向量方法证明空间线面垂直关系的有关定理.知识点一 向量法判断线线垂直思考 若直线 l1的方向向量为 μ1=(1,3,2),直线 l2的方向向量为 μ2=(1,-1,1),那么两直线是否垂直?用向量法判断两条直线垂直的一般方法是什么? 梳理 设直线 l 的方向向量为 a=(a1,a2,a3),直线 m 的方向向量为 b=(b1,b2,b3),则l⊥m⇔________⇔________.知识点二 向量法判断线面垂直思考 若直线 l 的方向向量为 μ1=,平面 α 的法向量为 μ2=,则直线 l 与平面 α 的位置关系是怎样的?如何用向量法判断直线与平面的位置关系?梳理 设直线 l 的方向向量 a=(a1,b1,c1),平面 α 的法向量 μ=(a2,b2,c2),则l⊥α⇔a∥μ⇔________.知识点三 向量法判断面面垂直思考 平面 α,β 的法向量分别为 μ1=(x1,y1,z1),μ2=(x2,y2,z2),用向量坐标法表示两平面 α,β 垂直的关系式是什么?梳理 若平面 α 的法向量为 μ=(a1,b1,c1),平面 β 的法向量为 ν=(a2,b2,c2),则α⊥β⇔μ⊥ν⇔μ·ν=0⇔________________.类型一 证明线线垂直例 1 已知正三棱柱 ABC-A1B1C1的各棱长都为 1,M 是底面上 BC 边的中点,N 是侧棱 CC1上的点,且 CN=CC1.求证:AB1⊥MN.反思与感悟 证明两直线垂直的基本步骤:建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.跟踪训练 1 如图,在直三棱柱 ABC-A1B1C1 中,AC=3,BC=4,AB=5,AA1=4,求证:AC⊥BC1.类型二 证明线面垂直例 2 如图所示,正三棱柱 ABC-A1B1C1的所有棱长都为 2,D 为 CC1的中点.求证:AB1⊥平面 A1BD.反思与感悟 用坐标法证明线面垂直的方法及步骤方法一:(1)建立空间直角坐标系.(2)将直线的方向向量用坐标表示.(3)找出平面内两条相交直线,并用坐标表示它们的方向向量.(4)分别计算两组向量的数量积,得到数量积为 0.方法二:(1)建立空间直角坐标系.(2)将直线的方向向量用坐标表示.(3)求出平面的法向量.(4)判断直线的方向向量与平面的法向量平行.跟踪训练 2 如图,在长方体 ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点 P 为 DD1的中点.求证:直线 PB1⊥平面 PAC.类型三 证明面面垂直例 3 在三...