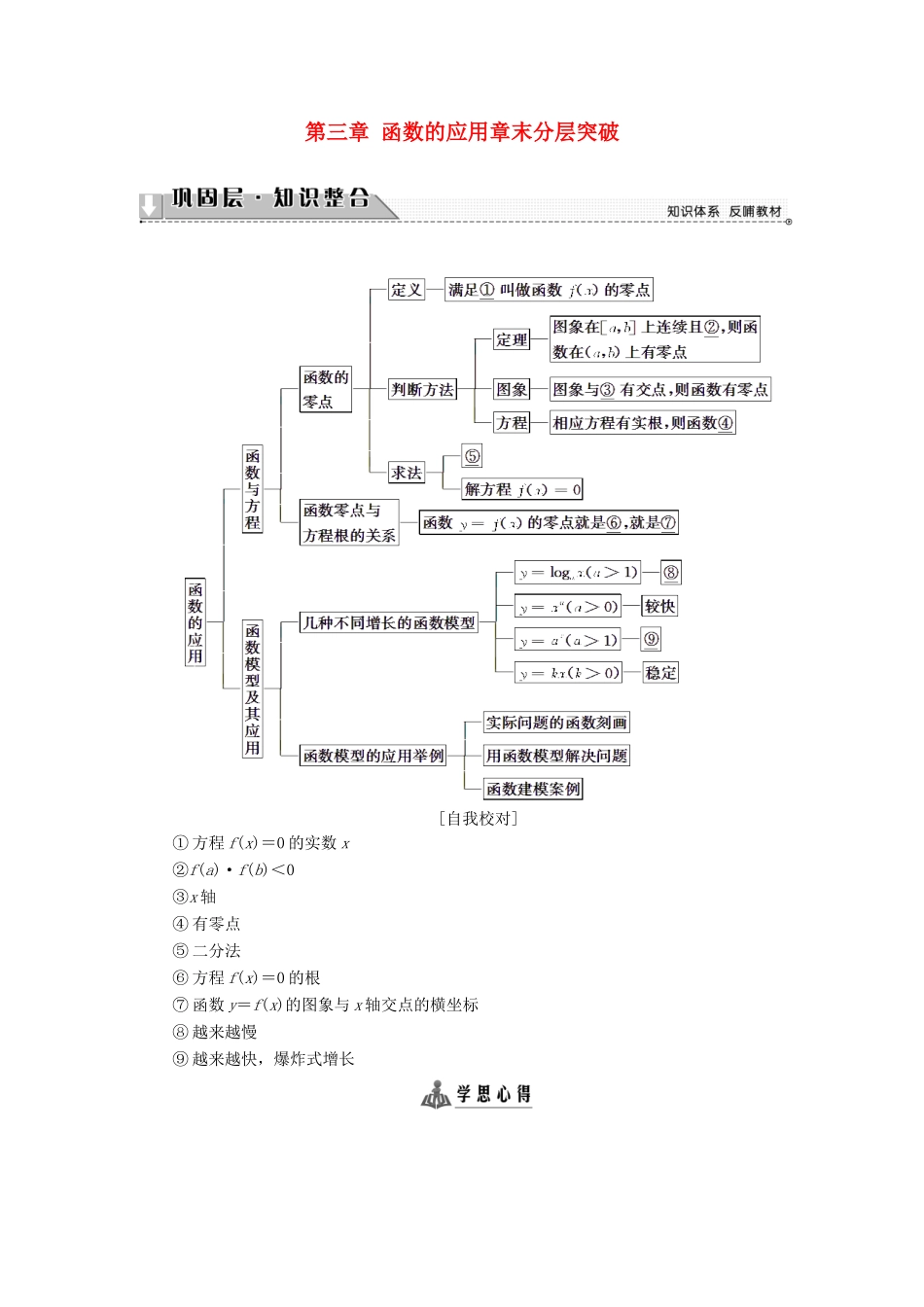
第三章 函数的应用章末分层突破[自我校对]① 方程 f(x)=0 的实数 x②f(a)·f(b)<0③x 轴④ 有零点⑤ 二分法⑥ 方程 f(x)=0 的根⑦ 函数 y=f(x)的图象与 x 轴交点的横坐标⑧ 越来越慢⑨ 越来越快,爆炸式增长函数的零点与方程的根1.方程 f(x)=0 有实数根⇔函数 y=f(x)的图象与 x 轴有交点⇔函数 y=f(x)有零点,在解决函数与方程问题时,要注意三者之间的关系,在解题中要充分利用这个关系实现问题的转化,同时还要注意使用函数的性质,如函数的单调性、奇偶性等.2.确定函数零点的个数或所在区间的两个基本方法:(1)利用零点的存在性定理,(2)数形结合转化为函数图象的交点问题. 函数 f(x)=x-的零点所在区间为( )A. B.C. D.(1,2)【精彩点拨】 利用零点判定定理分别判断端点值的符号关系.【规范解答】 f=-<0,f=->0,∴ff<0.所以,函数的零点所在的区间为,故选 B.【答案】 B[再练一题]1.设函数 f(x)是定义在 R 上的奇函数,当 x>0 时,f(x)=ex+x-3,则 f(x)的零点个数为( )A.1 B.2 C.3 D.4【解析】 函数 f(x)是定义域为 R 的奇函数,∴f(0)=0,所以 0 是函数 f(x)的一个零点,当 x>0 时,令 f(x)=ex+x-3=0,则 ex=-x+3,分别画出函数 y=ex,和 y=-x+3 的图象,如图所示,有一个交点,所以函数 f(x)有一个零点,又根据对称性知,当x<0 时,函数 f(x)也有一个零点.综上所述,f(x)的零点个数为 3 个,故选 C.【答案】 C函数模型的建立与应用建立函数模型的关键是根据条件找到关于变量的等式,建模的重点和难点是把实际问题抽象为数学问题的过程,仔细分析语言描述,要求什么,它等于什么,如何去表达,怎样求解,从中抽象出函数关系式,常见的函数模型如下表所示:常用函数模型(1)一次函数模型y=kx+b(2)二次函数模型y=ax2+bx+c(3)指数函数模型y=abx+c(4)对数函数模型y=mlogax+n(5)幂函数模型y=axn+b(6)分段函数y= 某商品在近 30 天内,每件的销售价格 P(元)与时间 t(天)的函数关系是:P = 该 商 品 的 日 销 售 量 Q( 件 ) 与 时 间 t( 天 ) 的 函 数 关 系 是 Q = - t + 40(0 <t≤30,t∈N),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是 30 天中的哪一天?【精彩点拨】 设日销售金额为 y 元,根据 y=PQ 写出函数 y 的解析式,再分类讨论:当 0<t≤...