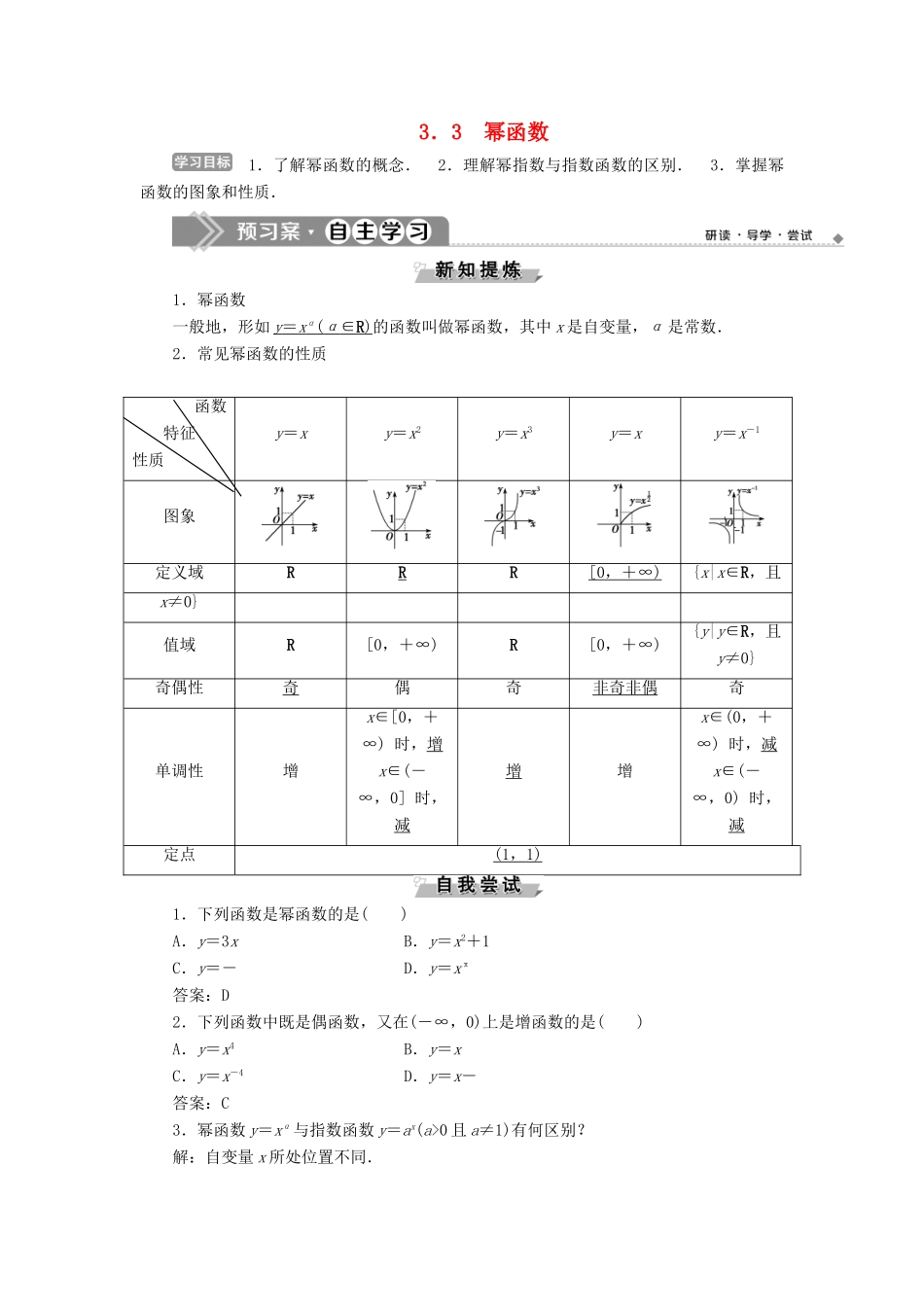
3.3 幂函数 1.了解幂函数的概念. 2.理解幂指数与指数函数的区别. 3.掌握幂函数的图象和性质.1.幂函数一般地,形如 y = x α ( α ∈ R ) 的函数叫做幂函数,其中 x 是自变量,α 是常数.2.常见幂函数的性质函数特征性质y=xy=x2y=x3y=xy=x-1图象定义域RRR[0 , +∞ ) {x|x∈R,且x≠0}值域R[0,+∞)R[0,+∞){y|y∈R,且y≠0}奇偶性奇偶奇非奇非偶奇单调性增x∈[0,+∞) 时,增x∈(-∞,0] 时,减增增x∈(0,+∞) 时,减x∈(-∞,0) 时,减定点(1 , 1 ) 1.下列函数是幂函数的是( )A.y=3x B.y=x2+1C.y=- D.y=xπ答案:D2.下列函数中既是偶函数,又在(-∞,0)上是增函数的是( )A.y=x4 B.y=xC.y=x-4 D.y=x-答案:C3.幂函数 y=xα与指数函数 y=ax(a>0 且 a≠1)有何区别?解:自变量 x 所处位置不同. 幂函数的概念 已知函数 f(x)=(m2+2m-2)xm2-m-1 是幂函数,则 m=________.【解析】 由题意知,若 f(x)为幂函数,则 m2+2m-2=1.即 m2+2m-3=0,解得 m=1 或 m=-3.【答案】 1 或-3判断幂函数的依据形如 y=xα(α∈R)的函数叫做幂函数,它具有三个特点: (1)系数为 1.(2)指数为一常数(也可以为 0).(3)后面不加任何项. 在下列给出的函数:① y=;② y=;③ y=x2+x 中,幂函数的个数为( )A.0 B.1C.2 D.3解析:选 C.y==x,y==x-2都是幂函数,而 y=x2+x 不是幂函数,故选 C. 幂的大小比较 比较下列各组数的大小:(1)3-和 3.1-;(2)-8-和-();(3)(-)-和(-)-;(4)4.1,3.8-和(-1.9).【解】 (1)因为函数 y=x-在(0,+∞)上为减函数,又因为 3<3.1,所以 3->3.1-.(2)-8-=-(),因为函数 y=x 在(0,+∞)上为增函数,又因为>,所以()>(),从而-()<-(),即-8-<-().(3)(-)-=()-,(-)-=()-,因为函数 y=x-在(0,+∞)上为减函数,又因为>,所以()-<()-,即(-)-<(-)-.(4)因为 4.1>1=1,0<3.8-<1-=1,(-1.9)<0,所以(-1.9)<3.8-<4.1.幂值比较大小常用的方法要比较的两个幂值的大小,若指数相同,底数不同时,考虑应用幂函数的单调性;若底数相同,指数不同时,考虑应用指数函数的单调性;若底数,指数均不相同,考虑借助中间量“1”,“0”,“-1”进行比较. 试比较,,三个数的大小.解:因为函数 ...