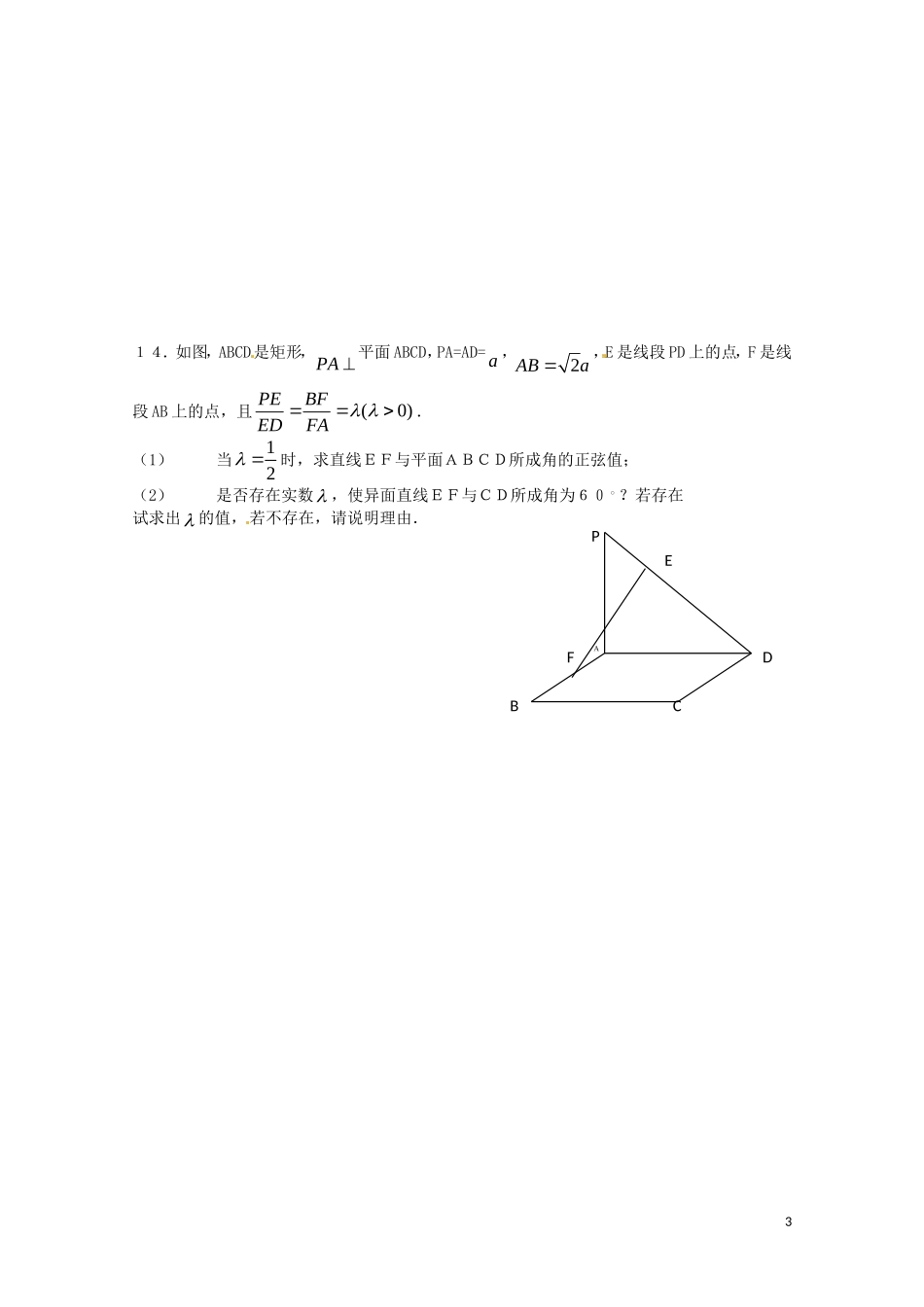
第 3 章 空间向量与立体几何复习题B组1.对于空间任意一点 O 和不共线的三点 A,B,C, ( , ,)x y zR,则1xyz 是P、A、B、C 四点共面的 ( ) A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件2.从点 A(2,-1,7)沿向量(8,9, 12)a 的方向取线段长|| 34AB �,则 B 点坐标为( )A.(-9,-7,7) B.(18,17,-17) C.(9,7,-7) D.(-14,-19,31)3.已知 P(3cos,3sin,1), (2cos,2sin,1)Q,则 PQ�取值范围是( ) A.0,5 B.0,25 C.1,5 D.1,54.已知空间四边形 ABCD 的每条 边和对角线的长都等于a ,点 E、F 分别是 BC、AD 的中点,则AEAF�的值为A.2a B.212 a C.214 a D.234 a5.已知 A(1,-2,11),B(4,2,3),C(6,-1,4),则 ABC的形状是( )A. 直角三角形 B.锐角三角形 C.钝角三角形 D.等腰直 角三角形6.平行六面体1111ABCDA B C D中,若1123,ACxAByBCzCC�则 xyz( )A.1 B. 76 C. 56 D. 237.自半径为 R 的球面上一点 P 引球的两两垂直的弦 PA、PB、PC,则 PA2+PB2+PC2 = ;8.已知(2, 1, ),(1,2,2),,60 ,ax ba b求实数 x =_______;9向量a 是平面 的法向量,也是直线l 的方向向量,则l与的关系是 ;10.已知1212(1,1,0),(1,1,1),,// ,,abbbbba ba��若且1_______b �则, 2______b �;11.如图,在空间四边形 ABCD 中,AB、BC、BD 两两垂直,且 AB=BC=2,E 是 AC 的中点,异面直线 AD 和 BE 的夹角为10arccos 10,求 BD 的长度. 1DCAzyxB12.在棱长AB=AD=2,1AA =3的长方体ABCD-1111A B C D 中,点E是平面11BCC B 内的动点,点F是CD的中点.(1)试确定点E的位置,使11D EAB F 平面; (2)求二面角1BAFB的大小. 13.如图,已知四棱锥 P-ABCD 的底面是直角梯形,90 ,ABCBCD2,ABBCPBPCCDPBCABCD侧面底面.(1)PA 与 BD 是否互相垂直?请证明你的结论;(2)求二面角 P-BD-C 的大小;(3)求证:平面 PAD 平面 PAB.2ABCPD14.如图,ABCD是矩形,PA 平面 ABCD,PA=AD=a ,2ABa,E 是线段 PD 上的点,F 是线段 AB 上的点,且(0)PEBFEDFA...