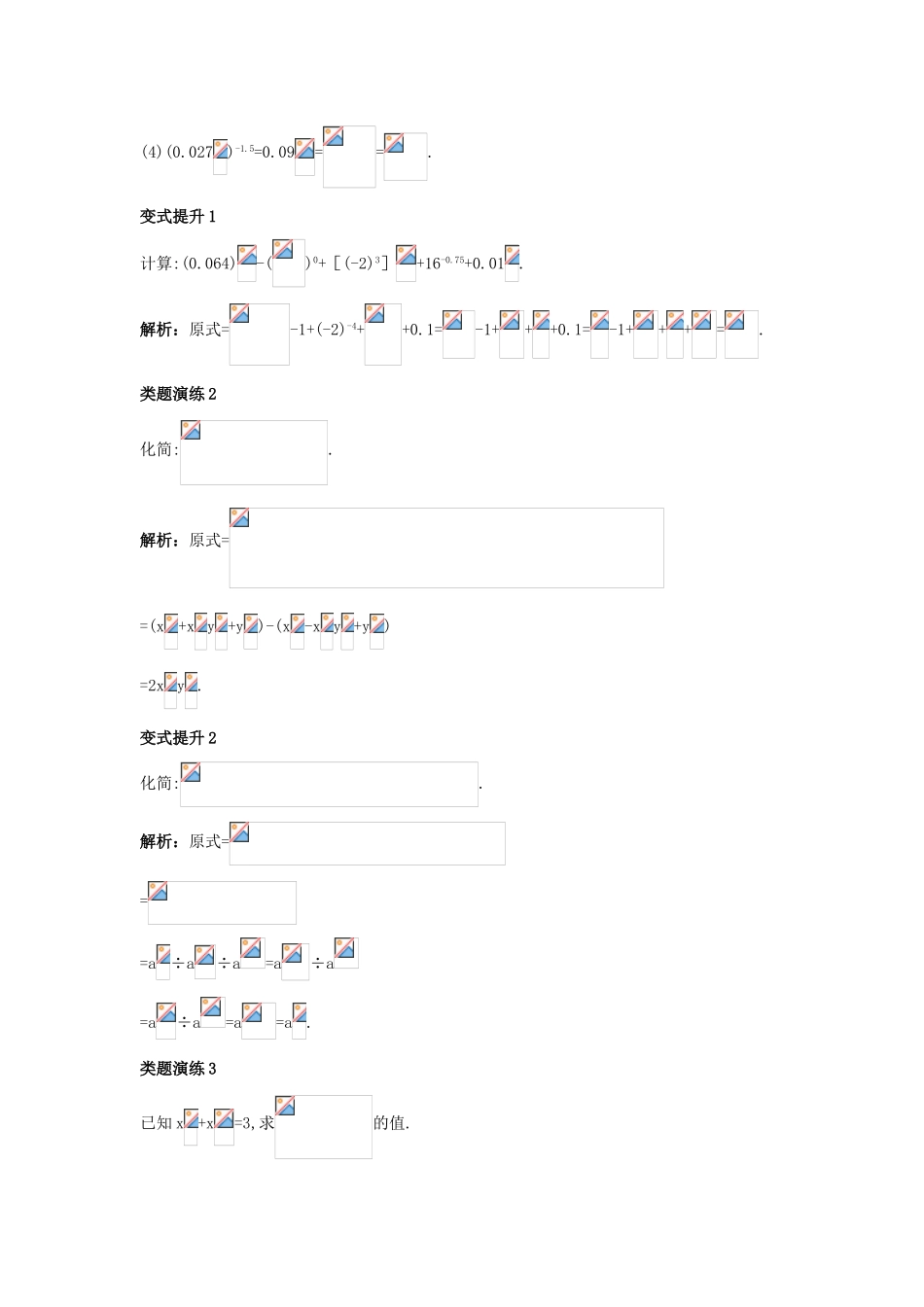
3.1.1 有理指数幂及其运算课堂导学三点剖析一、有理指数幂的计算【例 1】计算:()0.5+0.1-2+()-3π0+,解析:原式=()++()-3+=+100+-3+=100.温馨提示 利用分数指数幂的运算性质进行运算,需先化简,直至计算出最简结果,要在记准、记熟运算性质的基础上,结合具体问题灵活地运用.二、有理指数幂运算法则的应用【例 2】化简:÷()×.解析:原式===.温馨提示(1)本题化简的关键是 a-8b=(a )3-(2b )3=(a -2b )×(a+2a b +4b).(2)在指数式运算中,根式的化简,一般先化为分数指数幂,利用幂的运算法则进行运算与化简,一定要注意运算顺序和灵活运用乘法公式.三、有理指数幂运算法则的综合应用【例 3】(1)比较,,的大小;(2)已知 a+a=3,求的值.思路分析:(1)因根指数都不相同,应化成统一的根指数,再进行比较.(2)将所求式子化简,便可找到所求与条件的联系.解:(1)∵==,==,又∵121<123<125,∴<<.∴>>.(2)∵+a=3,∴平方得 a+a-1=7.∴==a+a-1+1=8.温馨提示(1)根式比较大小,当根指数相同时,只需比较被开方数的大小,被开方数大的根式的值大;当根指数不尽相同时,应先化成同次根式,再比较它们的大小.(2)分析所求与条件的关系,抓联系,消差异,促转化.各个击破类题演练 1计算:(1);(2);(3)(a>b);(4)(0.027)-1.5.解析:(1)=-8;(2)=10;(3)=|a-b|=a-b(a>b);(4)(0.027)-1.5=0.09==.变式提升 1计算:(0.064)-()0+[(-2)3]+16-0.75+0.01.解析:原式=-1+(-2)-4++0.1=-1+++0.1=-1+++=.类题演练 2化简:.解析:原式==(x+x y +y)-(x-x y +y)=2x y .变式提升 2化简:.解析:原式===a÷a÷a=a÷a=a÷a=a=a.类题演练 3已知 x+x=3,求的值.解析:由 x+x=3,两边平方得 x+x-1=7,再平方得 x2+x-2=47.又 x+x=(x+x)(x-1+x-1)=3×6=18,故==.变式提升 3已知 a、b 是方程 x2-6x+4=0 的两根,且 a>b>0,求的值.解析:∵a、b 是方程 x2-6x+4=0 的两根,∴∵a>b>0,∴,()2===.∴==.