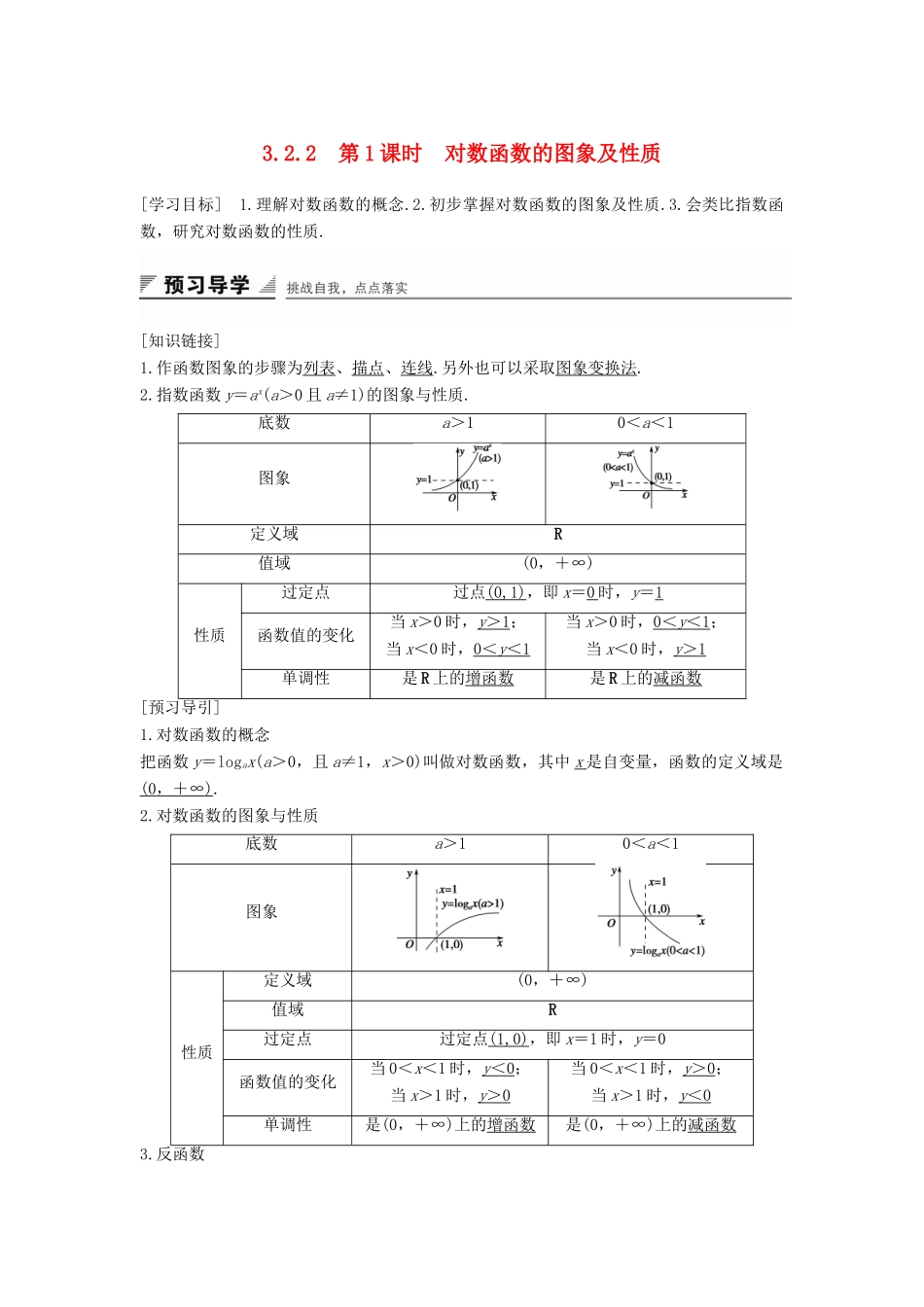
3.2.2 第 1 课时 对数函数的图象及性质[学习目标] 1.理解对数函数的概念.2.初步掌握对数函数的图象及性质.3.会类比指数函数,研究对数函数的性质.[知识链接]1.作函数图象的步骤为列表、描点、连线.另外也可以采取图象变换法.2.指数函数 y=ax(a>0 且 a≠1)的图象与性质.底数a>10<a<1图象定义域R值域(0,+∞)性质过定点过点(0,1),即 x=0 时,y=1函数值的变化当 x>0 时,y > 1 ;当 x<0 时,0 < y < 1 当 x>0 时,0 < y < 1 ;当 x<0 时,y > 1 单调性是 R 上的增函数是 R 上的减函数[预习导引]1.对数函数的概念把函数 y=logax(a>0,且 a≠1,x>0)叫做对数函数,其中 x 是自变量,函数的定义域是(0 ,+∞ ) .2.对数函数的图象与性质底数a>10<a<1图象性质定义域(0,+∞)值域R过定点过定点(1,0),即 x=1 时,y=0函数值的变化当 0<x<1 时,y < 0 ;当 x>1 时,y > 0 当 0<x<1 时,y > 0 ;当 x>1 时,y < 0 单调性是(0,+∞)上的增函数是(0,+∞)上的减函数3.反函数对数函数 y=logax(a>0 且 a≠1)与指数函数 y = a x ( a > 0 ,且 a ≠1) 互为反函数.要点一 对数函数的概念例 1 指出下列函数哪些是对数函数?(1)y=3log2x;(2)y=log6x;(3)y=logx3;(4)y=log2x+1解 (1)log2x 的系数是 3,不是 1,不是对数函数.(2)符合对数函数的结构形式,是对数函数.(3)自变量在底数位置上,不是对数函数.(4)对数式 log2x 后又加 1,不是对数函数.规律方法 判断一个函数是对数函数必须是形如 y=logax(a>0 且 a≠1)的形式,即必须满足以下条件(1)系数为 1.(2)底数为大于 0 且不等于 1 的常数.(3)对数的真数仅有自变量 x.跟踪演练 1 若某对数函数的图象过点(4,2),则该对数函数的解析式为( )A.y=log2x B.y=2log4xC.y=log2x 或 y=2log4x D.不确定答案 A解析 设对数函数的解析式为 y=logax(a>0 且 a≠1),由题意可知 loga4=2,∴a2=4,∴a=2,∴该对数函数的解析式为 y=log2x.要点二 对数函数的图象例 2 如图所示,曲线是对数函数 y=logax 的图象,已知 a 取,,,,则相应于 c1、c2、c3、c4的 a 值依次为( )A.、、、B.、、、C.、、、D.、、、答案 A解析 方法一 观察在(1,+∞)上的图象,先排 c1、c2底的顺序,底都大于 1,当 x>1 时图象靠近 x 轴的底大,c1...