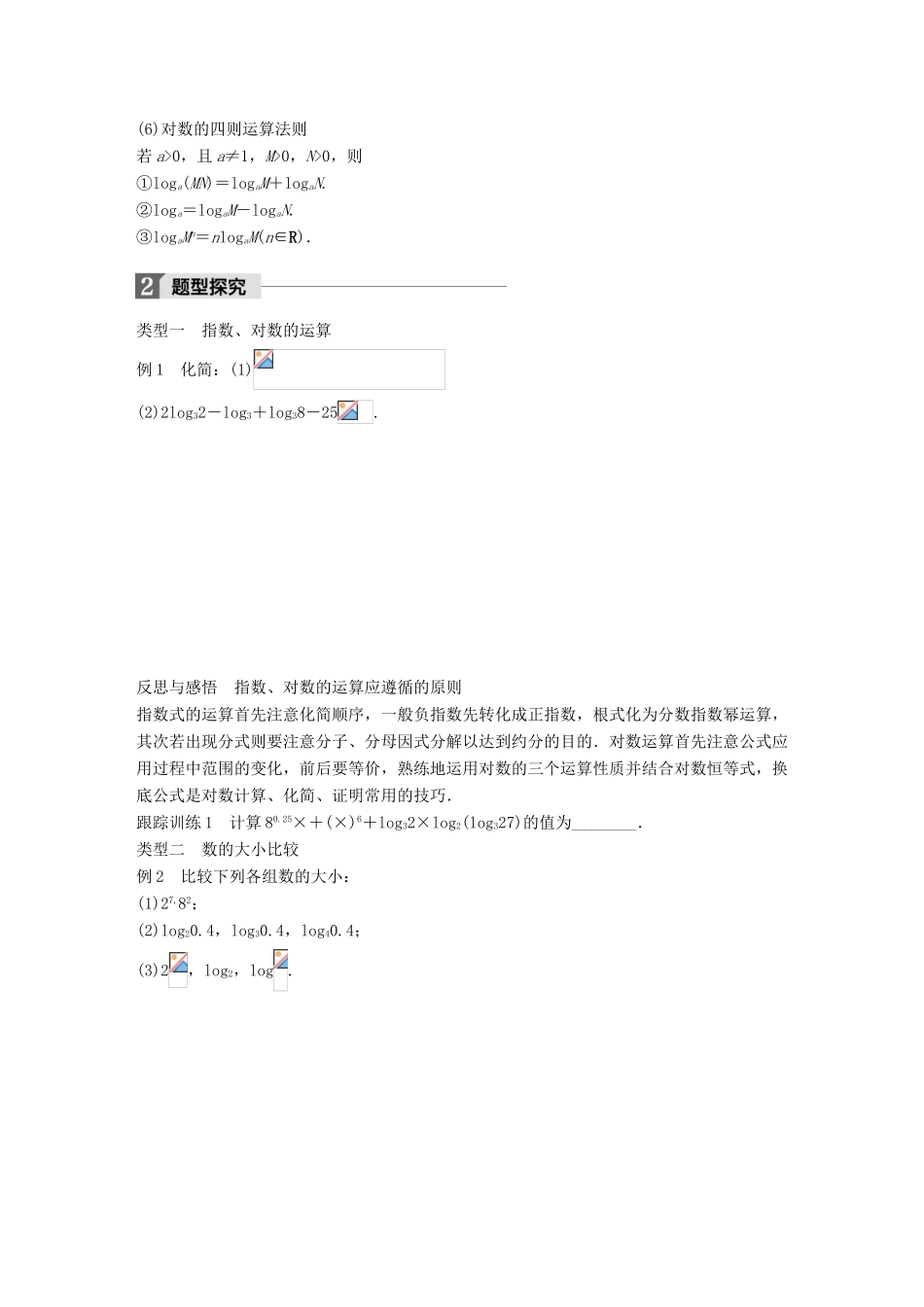
第三章 基本初等函数(Ⅰ)学习目标 1.构建知识网络.2.进一步熟练指数、对数运算,加深对公式成立条件的记忆.3.以函数观点综合理解指数函数、对数函数、幂函数.1.知识网络2.要点归纳(1)分数指数幂①a=(a>0,m,n∈N+,且 n>1).②a= (a>0,m,n∈N+,且 n>1).(2)根式的性质①()n=a.② 当 n 为奇数时, =a;当 n 为偶数时,=|a|=(3)指数幂的运算性质①ar·as=ar+s(a>0,r,s∈R).②(ar)s=ars(a>0,r,s∈R).③(ab)r=arbr(a>0,b>0,r∈R).(4)指数式与对数式的互化式logaN=b⇔ab=N(a>0,且 a≠1,N>0).(5)对数的换底公式logaN=(a>0,且 a≠1,m>0,且 m≠1,N>0).推论:logambn=logab(a>0,且 a≠1,m,n>0,且 m≠1,n≠1,b>0).(6)对数的四则运算法则若 a>0,且 a≠1,M>0,N>0,则①loga(MN)=logaM+logaN.②loga=logaM-logaN.③logaMn=nlogaM(n∈R).类型一 指数、对数的运算例 1 化简:(1)(2)2log32-log3+log38-25. 反思与感悟 指数、对数的运算应遵循的原则指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.跟踪训练 1 计算 80.25×+(×)6+log32×log2(log327)的值为________.类型二 数的大小比较例 2 比较下列各组数的大小:(1)27,82;(2)log20.4,log30.4,log40.4;(3)2,log2,log. 反思与感悟 数的大小比较常用方法:(1)比较两数(式)或几个数(式)大小问题是本章的一个重要题型,主要考查指数函数、对数函数、幂函数图象与性质的应用及差值比较法与商值比较法的应用.常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于 0”,“大于等于 0 小于等于 1”,“大于 1”三部分,再在各部分内利用函数的性质比较大小.跟踪训练 2 比较下列各组数的大小:(1)log0.22,log0.049;(2)a1.2,a1.3;(3)30.4,0.43,log0.43. 类型三 指数函数、对数函数、幂函数的综合应用例 3 已知函数 f(x)=...