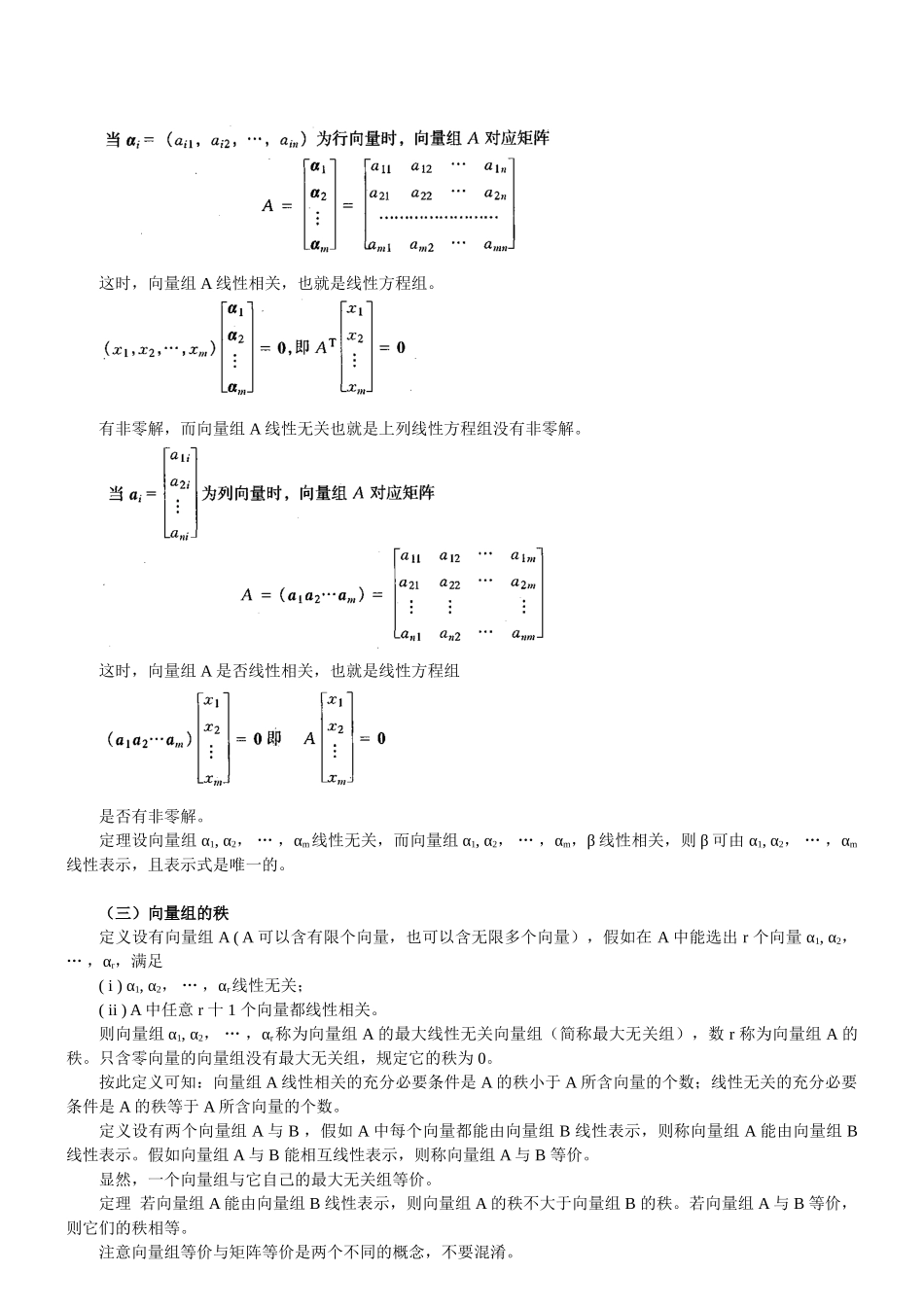
三、 n 维向量(一) n 维向量n 个有序数 al , a2 , … ,an所组成的数组α=(α1,α2…αn)称为 n 维向量。为了沟通向量与矩阵的联系,,维向量亦记作并把 α 称为行向量, a 称为列向量。行向量即行矩阵,列向量即列矩阵,规定向量与矩阵一样进行运算, αT = a , aT = "α;行向量与列向量不能相加。m 个 n 维列向量所组成的向量组可对应一个 n×m 矩阵反之,一个 m×n 矩阵 A 有 m 个 n 维行向量,这些行向量所组成的向量组称为矩阵 A 。的行向量组;同时, A 又有 n 个 m 维列向量,这些列向量所组成的向量组称为 A 的列向量组。(二)向量组的线性相关与线性无关定义 设有向量组 A : α1, α2, … ,αm 与向量 β ,假如有一组数 kl , k2, … , km使则称向量 β 是向量组 α1, α2, … ,αm的线性组合,或称 β 可由 α1, α2, … ,αm,线性表出定义设有向量组 A : α1, α2, … ,αm,假如有一组不全为 0 的数 kl , k2, … ,km使则说向量组 A 是线性相关的,否则说向量组 A 是线性无关的。这时,向量组 A 线性相关,也就是线性方程组。有非零解,而向量组 A 线性无关也就是上列线性方程组没有非零解。这时,向量组 A 是否线性相关,也就是线性方程组是否有非零解。定理设向量组 α1, α2, … ,αm线性无关,而向量组 α1, α2, … ,αm,β 线性相关,则 β 可由 α1, α2, … ,αm线性表示,且表示式是唯一的。(三)向量组的秩定义设有向量组 A ( A 可以含有限个向量,也可以含无限多个向量),假如在 A 中能选出 r 个向量 α1, α2, … ,αr,满足( i ) α1, α2, … ,αr线性无关;( ii ) A 中任意 r 十 1 个向量都线性相关。则向量组 α1, α2, … ,αr称为向量组 A 的最大线性无关向量组(简称最大无关组),数 r 称为向量组 A 的秩。只含零向量的向量组没有最大无关组,规定它的秩为 0。按此定义可知:向量组 A 线性相关的充分必要条件是 A 的秩小于 A 所含向量的个数;线性无关的充分必要条件是 A 的秩等于 A 所含向量的个数。定义设有两个向量组 A 与 B ,假如 A 中每个向量都能由向量组 B 线性表示,则称向量组 A 能由向量组 B 线性表示。假如向量组 A 与 B 能相互线性表示,则称向量组 A 与 B 等价。显然...