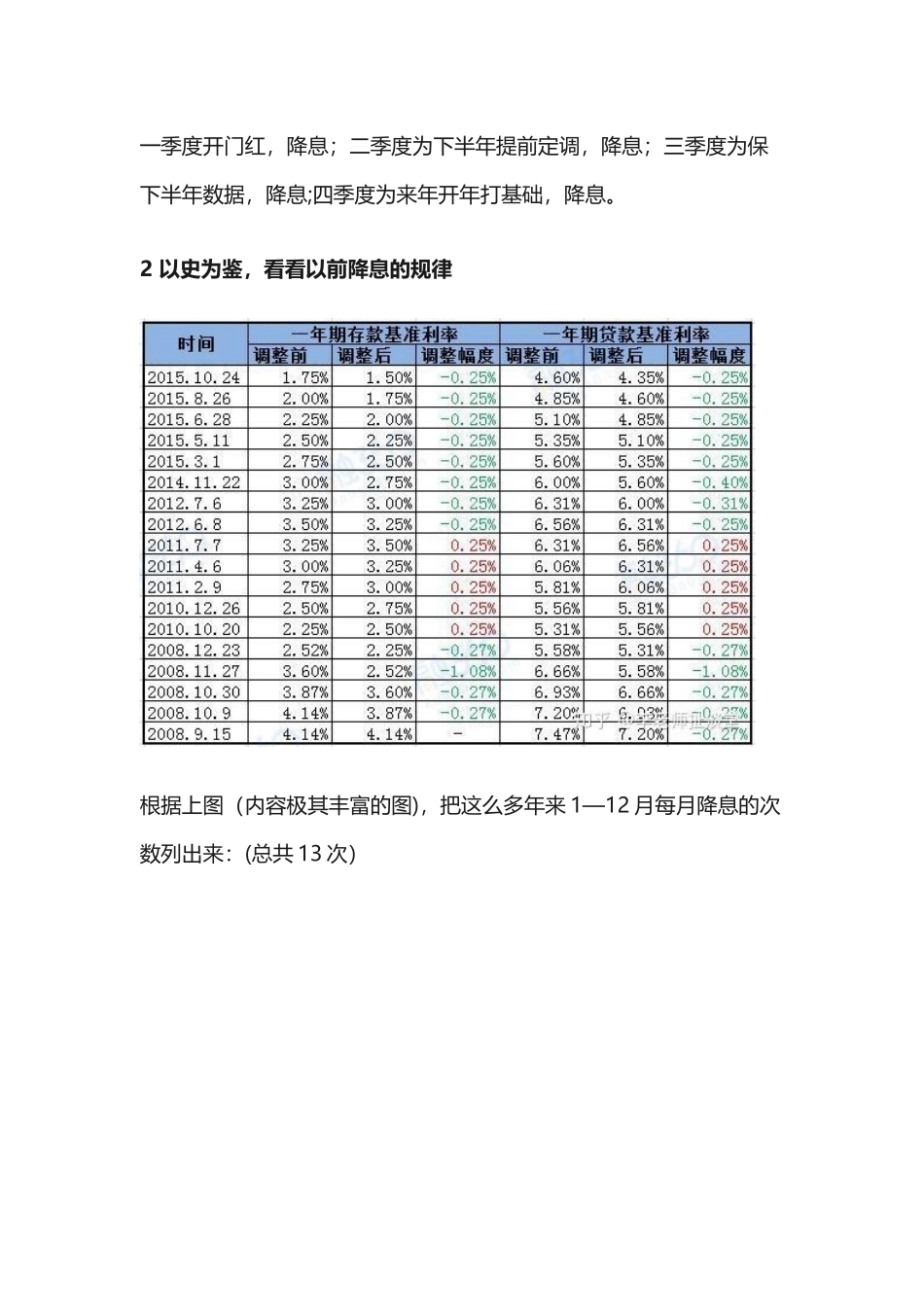
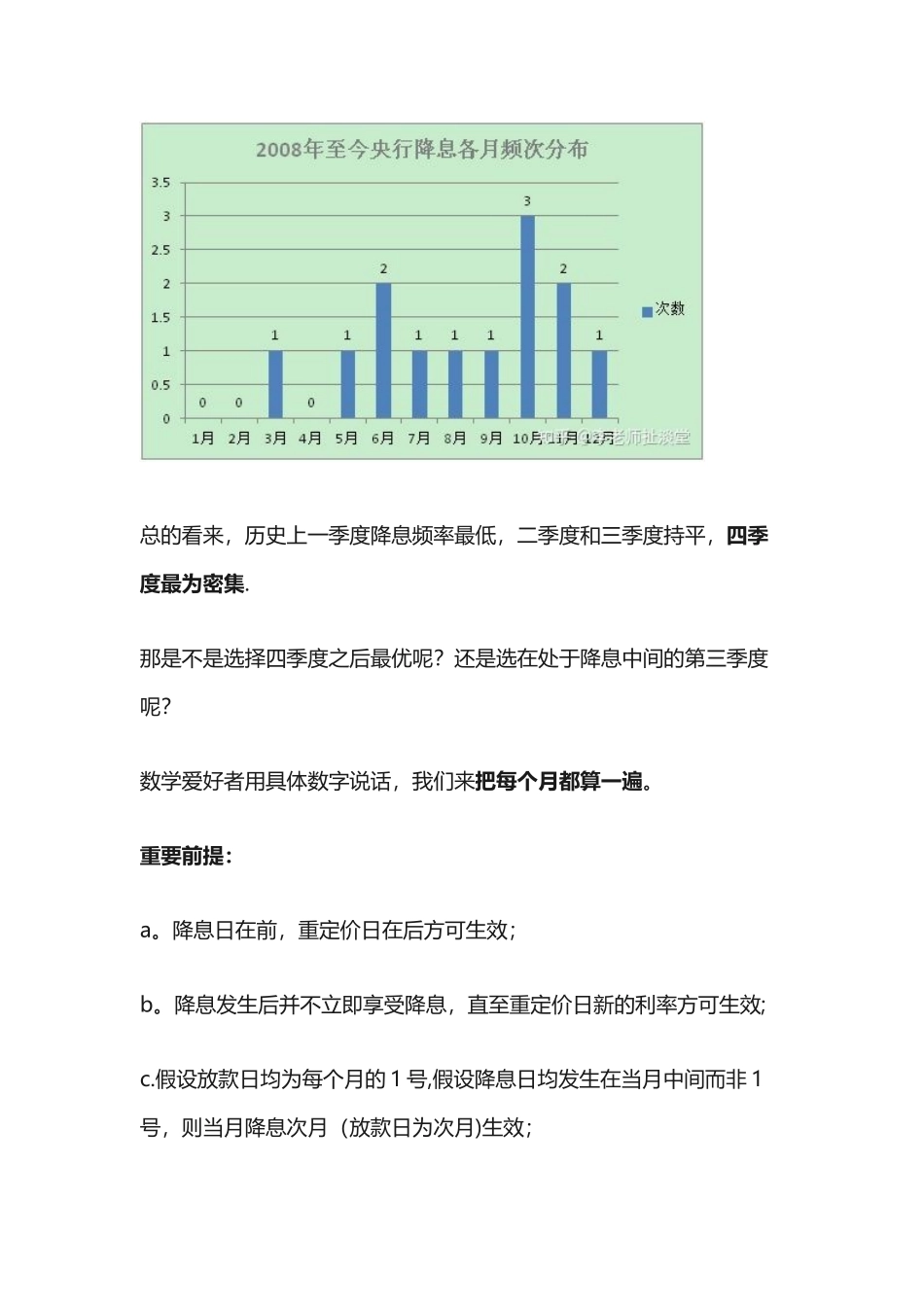
1 贷款利率不是紧随着 LPR 的变化而变化,是在 LPR 变化后的重定价日生效2 重定价日紧跟在降息日之后,可以尽早享受降息优惠3 如何在 2025 年大概率降息的眼下,根据自己的放款日来选择重定价日,尽快享受当下的降息优惠有了基本的推导思路,那么进一步思考:未来若干年到底降息是如何分布?如何得到最优选?1 预判未来降息规律降息的目的,通常是为了刺激经济、拉动经济,那么精确到月难度较大,而上半年下半年或者根据季度,就相对容易一丢丢.上半年发现数据跟不上,下半年拉,那么下半年概率大;今年数据不错但估量明年困难,开门红就降息拉动经济。一季度开门红,降息;二季度为下半年提前定调,降息;三季度为保下半年数据,降息;四季度为来年开年打基础,降息。2 以史为鉴,看看以前降息的规律根据上图(内容极其丰富的图),把这么多年来 1—12 月每月降息的次数列出来:(总共 13 次)总的看来,历史上一季度降息频率最低,二季度和三季度持平,四季度最为密集.那是不是选择四季度之后最优呢?还是选在处于降息中间的第三季度呢?数学爱好者用具体数字说话,我们来把每个月都算一遍。重要前提:a。降息日在前,重定价日在后方可生效;b。降息发生后并不立即享受降息,直至重定价日新的利率方可生效;c.假设放款日均为每个月的 1 号,假设降息日均发生在当月中间而非 1号,则当月降息次月(放款日为次月)生效;计算思路:当放款日落在 2—12 月时,逐一与 1 月 1 日进行对比,多付了几个月利息,减去,少付了几个月利息,得出付息月数,根据不同月付息月数的数字大小,逐一排序,得出历年降息占尽便宜的最优解.正式开始:2 月历史上 1 月未发生过降息,意味着每次降息,2 月都要比 1 月 1 日多付1 个月的利息。历史上降息次数为 13 次,那么假如放款日落在 2 月,选择重定价日为 2 月,比 1 月 1 日,累计多付 13 个月的利息。3 月历史上 1 月、2 月均无降息,意味着每次降息,3 月都要比 1 月 1 日多付 2 个月的利息.历史上降息次数为 13 次,那么假如放款日落在 3 月,选择重定价日为 3 月,比 1 月 1 日,累计多付 2*13=26 个月的利息。4 月历史上 1 月、2 月、3 月中,仅有 3 月发生过 1 次降息,此外 12 次均在 4 月以后,4 月比 1 月 1 日多付 3 个月的利息,那么多付的次数是 3*12=36 次;在 3 月发生的降息,4 月立即生效,而 1 月 1 日...