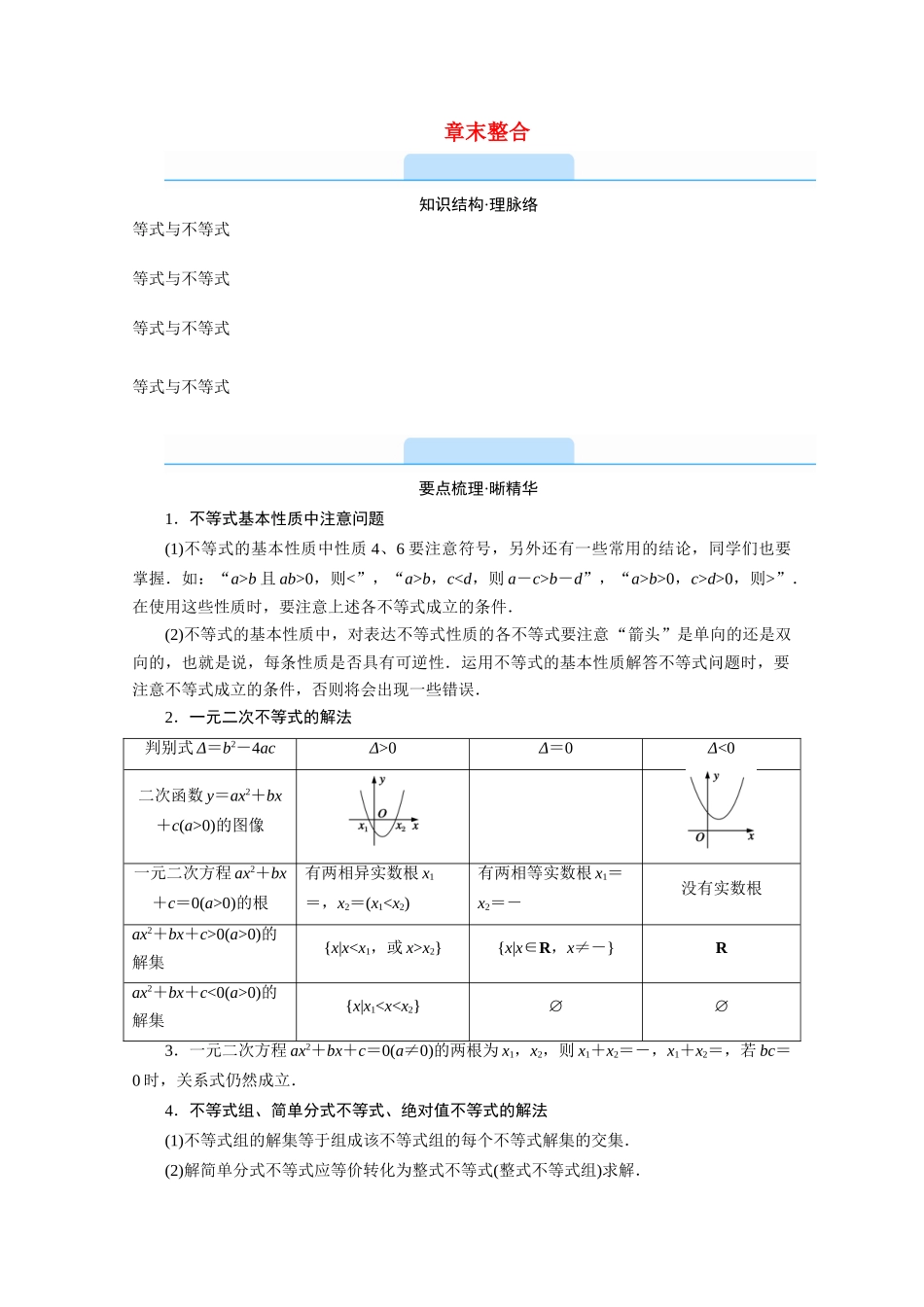
章末整合知识结构·理脉络等式与不等式等式与不等式等式与不等式等式与不等式要点梳理·晰精华1.不等式基本性质中注意问题(1)不等式的基本性质中性质 4、6 要注意符号,另外还有一些常用的结论,同学们也要掌握.如:“a>b 且 ab>0,则<”,“a>b,cb-d”,“a>b>0,c>d>0,则>”.在使用这些性质时,要注意上述各不等式成立的条件.(2)不等式的基本性质中,对表达不等式性质的各不等式要注意“箭头”是单向的还是双向的,也就是说,每条性质是否具有可逆性.运用不等式的基本性质解答不等式问题时,要注意不等式成立的条件,否则将会出现一些错误.2.一元二次不等式的解法判别式 Δ=b2-4acΔ>0Δ=0Δ<0二次函数 y=ax2+bx+c(a>0)的图像一元二次方程 ax2+bx+c=0(a>0)的根有两相异实数根 x1=,x2=(x10(a>0)的解集{x|xx2}{x|x∈R,x≠-}Rax2+bx+c<0(a>0)的解集{x|x10,b>0,那么≥,当且仅当 a=b 时,等号成立,即正数 a 与 b的算术平均数不小于它们的几何平均数.(2)几个常用的重要结论:①+≥2(a 与 b 同号,当且仅当 a=b 时取等号).②a+≥2(a>0,当且仅当 a=1 时取等号),a+≤-2(a<0,当且仅当 a=-1 时取等号).③ab≤()2(a,b∈R,当且仅当 a=b 时取等号).(3)利用均值不等式求最值已知 x>0,y>0,则① 如果积 xy 是定值 p,那么当且仅当 x=y 时,x+y 有最小值 2(简记:积定和最小).② 如果 x+y 是定值 s,那么当且仅当 x=y 时,xy 有最大值(简记:和定积最大).素养突破·提技能类型 特殊不等式的解法┃┃ 典例剖析 __■1.一元高次不等式的解法典例 1 解不等式:(x+2)(x2-x-12)>0.思路探究:可转化为不等式组或用数轴标根法两种方法求解.解析:方法一:原不等式可化为或即或解得 x>4 或-3