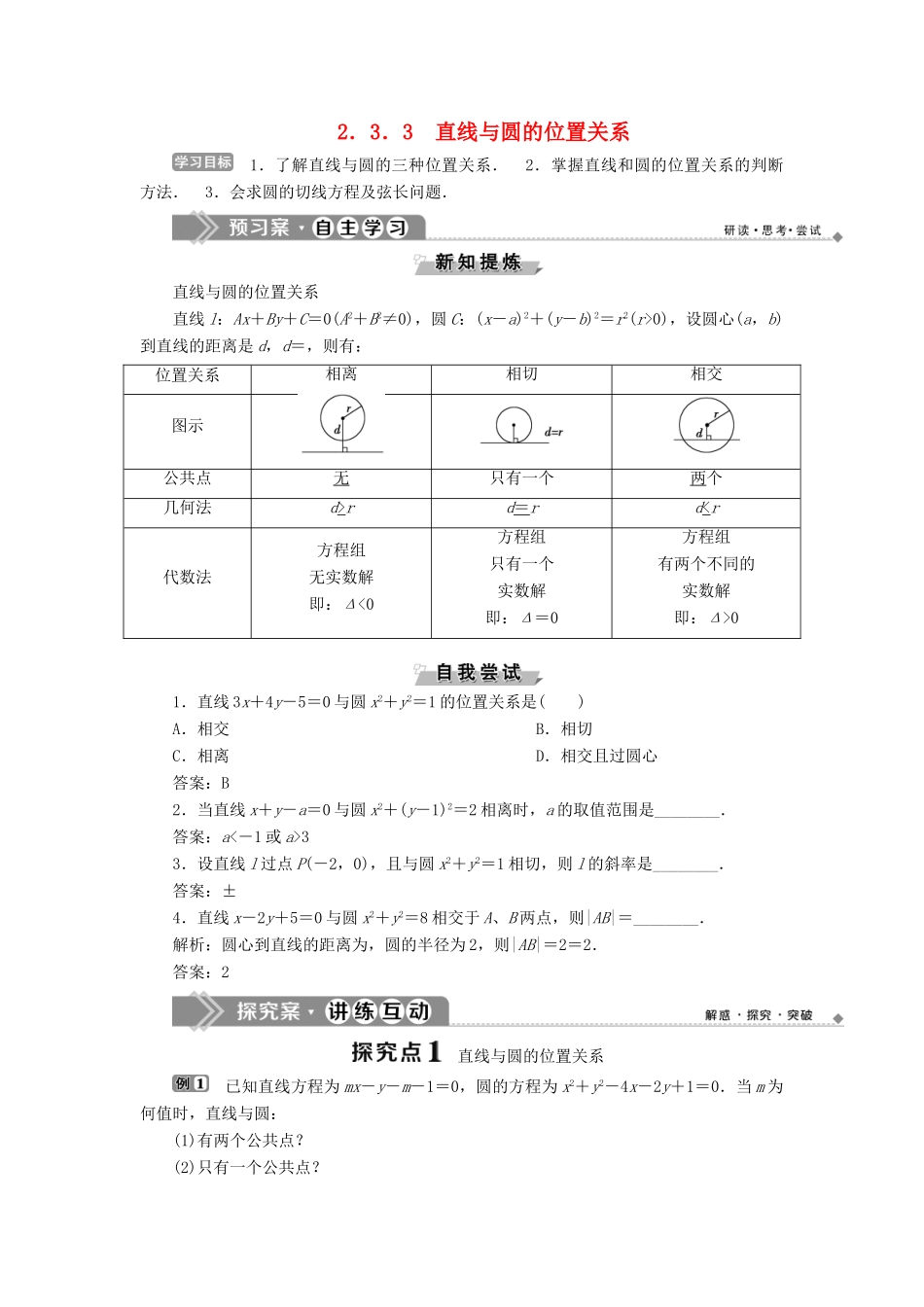
2.3.3 直线与圆的位置关系 1.了解直线与圆的三种位置关系. 2.掌握直线和圆的位置关系的判断方法. 3.会求圆的切线方程及弦长问题.直线与圆的位置关系直线 l:Ax+By+C=0(A2+B2≠0),圆 C:(x-a)2+(y-b)2=r2(r>0),设圆心(a,b)到直线的距离是 d,d=,则有:位置关系相离相切相交图示公共点无只有一个两个几何法d>rd=rd01.直线 3x+4y-5=0 与圆 x2+y2=1 的位置关系是( )A.相交 B.相切C.相离 D.相交且过圆心答案:B2.当直线 x+y-a=0 与圆 x2+(y-1)2=2 相离时,a 的取值范围是________.答案:a<-1 或 a>33.设直线 l 过点 P(-2,0),且与圆 x2+y2=1 相切,则 l 的斜率是________.答案:±4.直线 x-2y+5=0 与圆 x2+y2=8 相交于 A、B 两点,则|AB|=________.解析:圆心到直线的距离为,圆的半径为 2,则|AB|=2=2.答案:2 直线与圆的位置关系 已知直线方程为 mx-y-m-1=0,圆的方程为 x2+y2-4x-2y+1=0.当 m 为何值时,直线与圆:(1)有两个公共点?(2)只有一个公共点?(3)没有公共点?【解】 法一:将 mx-y-m-1=0 代入圆的方程,化简整理得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0,Δ=4m(3m+4),(1)当 Δ>0,即 m>0 或 m<-时,直线与圆相交,故直线与圆有两个公共点;(2)当 Δ=0,即 m=0 或 m=-时,直线与圆相切,故直线与圆只有一个公共点;(3)当 Δ<0,即-0 或 m<-时,直线与圆相交,故直线与圆有两个公共点;(2)当 d=2,即 m=0 或 m=-时,直线与圆相切,故直线与圆只有一个公共点;(3)当 d>2,即-