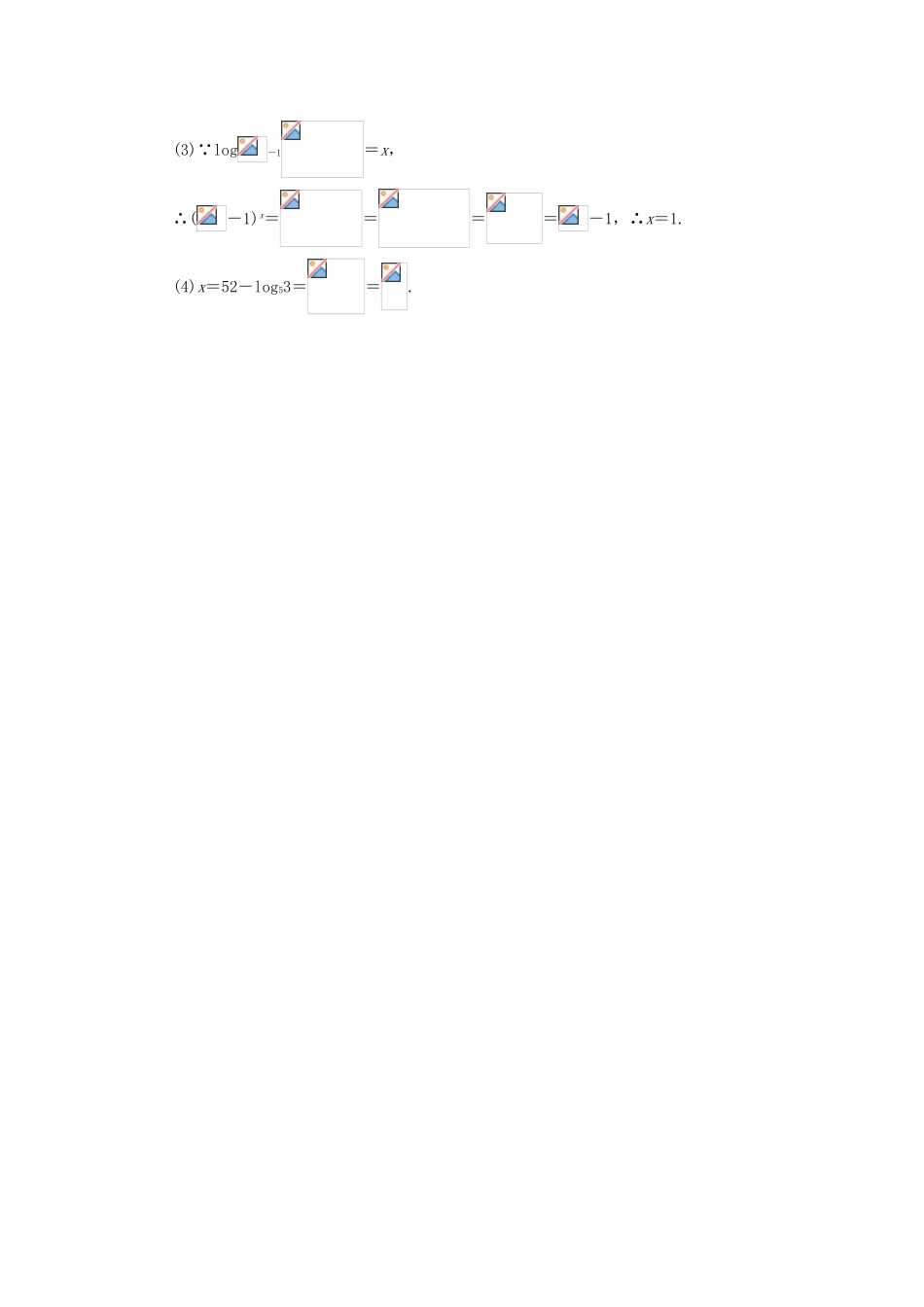
2.2 对数函数课堂探究探究一 对数式与指数式的互化1.logaN=b 与 ab=N(a>0,且 a≠1)是等价的,表示 a,b,N 三者之间的同一种关系.可以利用其中两个量表示第三个量.2.已知底数与指数或已知指数与幂时,通常用指数式求幂或底数;若已知底数与幂求指数,需用对数式,所以指数式与对数式的互化在幂的运算中经常用到.【典型例题 1】 将下列指数式与对数式互化:(1)log216=4; (2) =-3;(3)ln 10=2.303; (4)43=64;(5)3-2=; (6)10-3=0.001.思路分析:利用当 a>0,且 a≠1 时,logaN=b⇔ab=N 进行互化.解:(1)24=16.(2) -3=27.(3)e2.303=10.(4)log464=3.(5)log3=-2.(6)lg 0.001=-3.探究二 利用对数式与指数式的关系求值指数式 ax=N 与对数式 x=logaN(a>0,且 a≠1)表示了三个量 a,x,N 之间的关系,因而已知其中两个可求第三个:已知底数与指数,用指数式求幂;已知指数与幂,用指数式求底数;已知底数与幂,利用对数式表示指数.【典型例题 2】 求下列各式中 x 的值:(1)4x=5·3x;(2)log7(x+2)=2;(3)log=x;(4)logx27=;(5)lg 0.01=x.思路分析:利用指数式与对数式的关系求解.解:(1)∵4x=5·3x,∴=5,∴x=5,∴x=.(2)∵log7(x+2)=2,∴x+2=72=49,∴x=47.(3)∵-2=,∴log=-2,∴x=-2.(4)∵logx27=,∴=27,∴x==32=9.(5)∵lg 0.01=x,∴10x=0.01=10-2,∴x=-2.探究三 对数性质的应用1.对数的性质:(1)在指数式中 N>0,故零和负数没有对数.(2)设 a>0,a≠1,则有 a0=1.∴loga1=0,即 1 的对数等于 0.(3)设 a>0,a≠1,则有 a1=a,∴logaa=1,即底数的对数为 1.2.对数恒等式:alogaN=N,该式叫做对数恒等式.3.在对数的运算中,常用对数的性质和对数恒等式进行对数的化简与求值.【典型例题 3】 求下列各式中 x 的值:(1)log3(log2x)=0; (2)log2(lg x)=1;(3)log-1=x; (4)52-log53=x.思路分析:利用 logaa=1,loga1=0,alogaN=N(a>0,且 a≠1)及指数式与对数式的关系解题.解:(1)∵log3(log2x)=0,∴log2x=1,∴x=21=2.(2)∵log2(lg x)=1,∴lg x=2,∴x=102=100.(3)∵log-1=x,∴(-1)x====-1,∴x=1.(4)x=52-log53==.