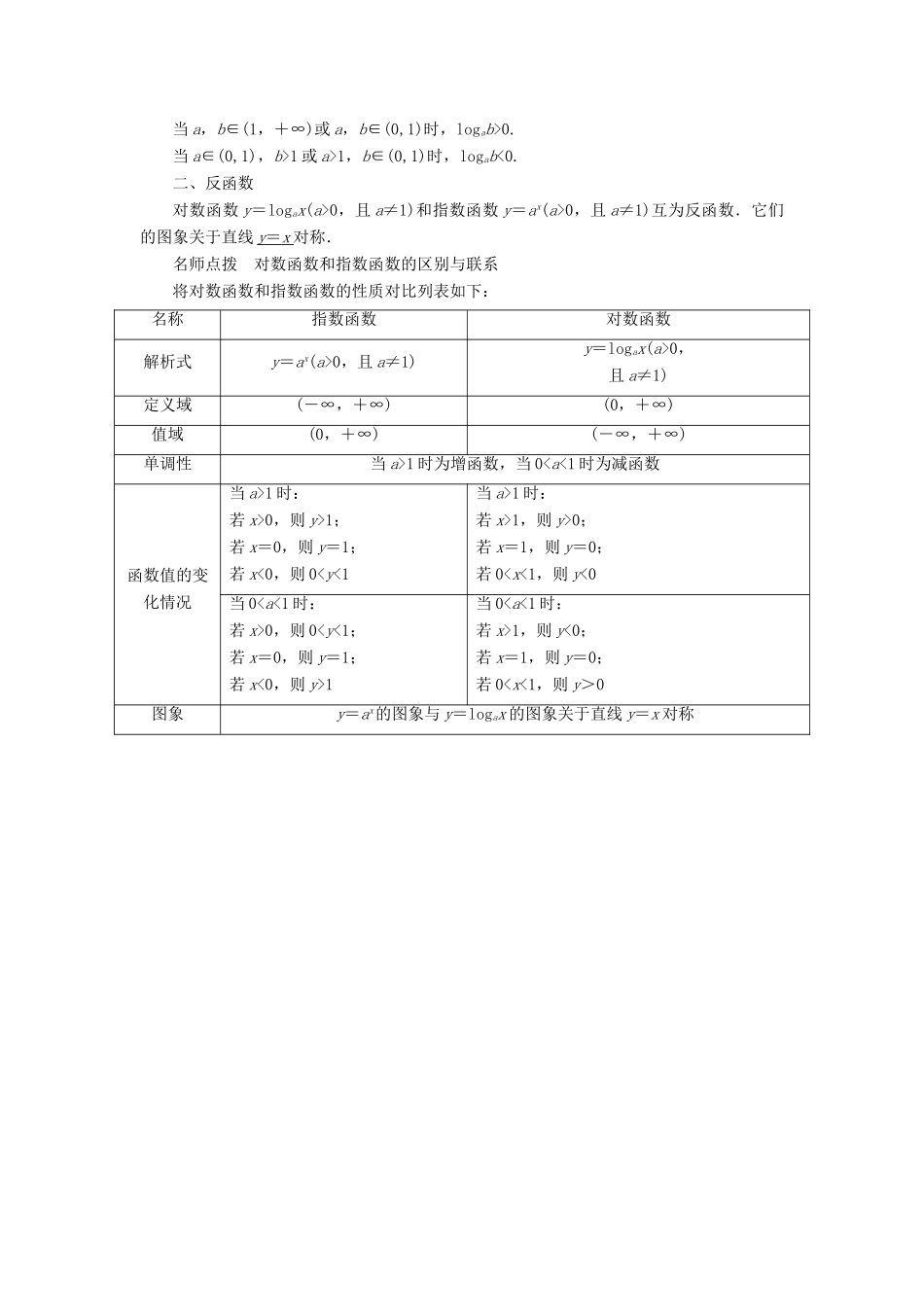
2.2 对数函数预习导航课程目标学习脉络1.掌握对数函数的概念,会判断对数函数.2.初步掌握对数函数的图象和性质.3.能利用对数函数的性质解决与对数函数有关的定义域、定点问题.一、对数函数名师点拨 1.对对数函数定义的理解:(1)由于指数函数 y=ax中的底数 a 满足 a>0,且 a≠1,则对数函数 y=logax 中的底数a 也必须满足 a>0,且 a≠1.(2)对数函数的解析式同时满足:①对数符号前面的系数是 1;②对数的底数是不等于1 的正实数(常数);③对数的真数仅有自变量 x.2.对数函数的图象:对数函数的图象,当 x 趋近于 0 时,无限接近于 y 轴,但不相交.作直线 y=1 与函数 y=logax 的图象相交,则交点横坐标为 a.自主思考 1 函数 y=logax(a>0,且 a≠1)的图象与函数 y=logx(a>0,且 a≠1)的图象有怎样的关系?提示:观察课本第 70 页图 2.23 知,两函数的图象关于 x 轴对称.事实上,函数 y=logax 图象上任一点 P(x,y)关于 x 轴的对称点 P′(x,-y)都在函数 y=logx 的图象上,所以这两个函数的图象关于 x 轴对称.自主思考 2a,b 在什么情况下,logab>0?什么情况下,logab<0?提示:观察对数函数图象知,当 a,b∈(1,+∞)或 a,b∈(0,1)时,logab>0.当 a∈(0,1),b>1 或 a>1,b∈(0,1)时,logab<0.二、反函数对数函数 y=logax(a>0,且 a≠1)和指数函数 y=ax(a>0,且 a≠1)互为反函数.它们的图象关于直线 y = x 对称.名师点拨 对数函数和指数函数的区别与联系将对数函数和指数函数的性质对比列表如下:名称指数函数对数函数解析式y=ax(a>0,且 a≠1)y=logax(a>0,且 a≠1)定义域(-∞,+∞)(0,+∞)值域(0,+∞)(-∞,+∞)单调性当 a>1 时为增函数,当 0
1 时:若 x>0,则 y>1;若 x=0,则 y=1;若 x<0,则 01 时:若 x>1,则 y>0;若 x=1,则 y=0;若 00,则 01当 01,则 y<0;若 x=1,则 y=0;若 0