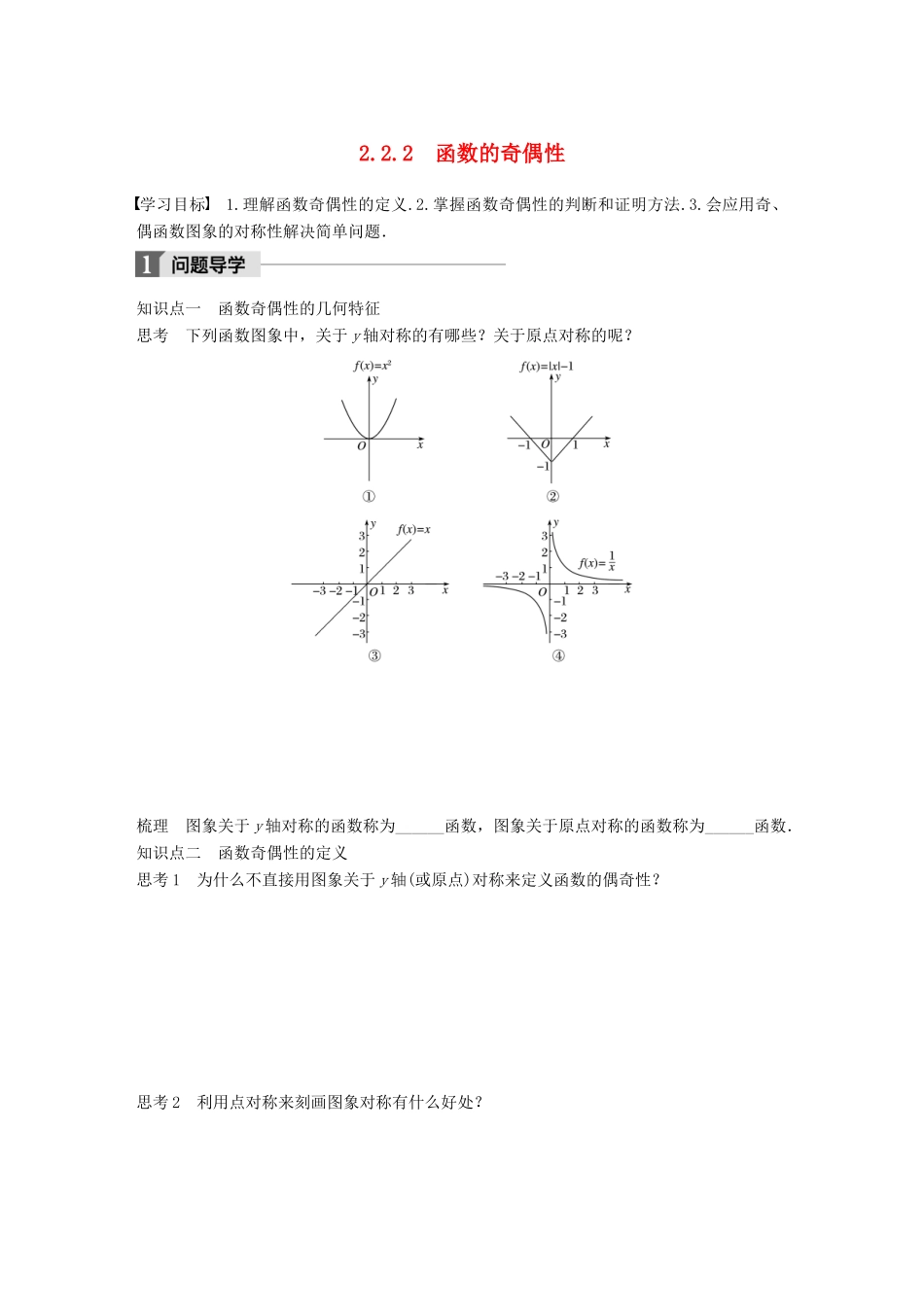
2.2.2 函数的奇偶性学习目标 1.理解函数奇偶性的定义.2.掌握函数奇偶性的判断和证明方法.3.会应用奇、偶函数图象的对称性解决简单问题.知识点一 函数奇偶性的几何特征思考 下列函数图象中,关于 y 轴对称的有哪些?关于原点对称的呢? 梳理 图象关于 y 轴对称的函数称为______函数,图象关于原点对称的函数称为______函数.知识点二 函数奇偶性的定义思考 1 为什么不直接用图象关于 y 轴(或原点)对称来定义函数的偶奇性? 思考 2 利用点对称来刻画图象对称有什么好处? 梳理 设函数 y=f(x)的定义域为 A.如果对于任意的 x∈A,都有 f(-x)=f(x),那么称函数 y=f(x)是偶函数;如果对于任意的 x∈A,都有 f(-x)=-f(x),那么称函数 y=f(x)是奇函数.如果函数 f(x)是奇函数或偶函数,我们就说函数 f(x)具有奇偶性.知识点三 奇(偶)函数的定义域特征思考 如果一个函数 f(x)的定义域是(-1,1],那这个函数 f(x)还具有奇偶性吗? 梳理 判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于________对称.类型一 证明函数的奇偶性命题角度 1 已知函数解析式,证明奇偶性例 1 (1)证明 f(x)=既非奇函数又非偶函数;(2)证明 f(x)=(x+1)(x-1)是偶函数;(3)证明 f(x)=+既是奇函数又是偶函数. 反思与感悟 利用定义法判断函数是否具有奇偶性时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个 x,则-x 也一定属于定义域.跟踪训练 1 (1)证明 f(x)=(x-2) 既非奇函数又非偶函数;(2)证明 命题角度 2 证明分段函数的奇偶性例 2 判断函数 f(x)=的奇偶性. 反思与感悟 分段函数也是函数,证明奇偶性也是抓住两点(1)定义域是否关于原点对称.(2)对于定义域内的任意 x,是否都有 f(-x)=f(x)(或-f(x)),只不过对于不同的x,f(x)有不同的表达式,要逐段验证是否都有 f(-x)=f(x)(或-f(x)).跟踪训练 2 证明 f(x)=是奇函数. 命题角度 3 证明抽象函数的奇偶性例 3 f(x),g(x)是定义在 R 上的奇函数,试判断 y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性. 反思与感悟 利用基本的奇(偶)函数,通过加减乘除、复合,可以得到新的函数,判断这些新函数的奇偶性,主要是代入-x,看总的结果.跟踪训练 3 设函数 f(x),g(x)的定义域都为 R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是______.(填序号)①f(x)g(x)是奇函数;②...