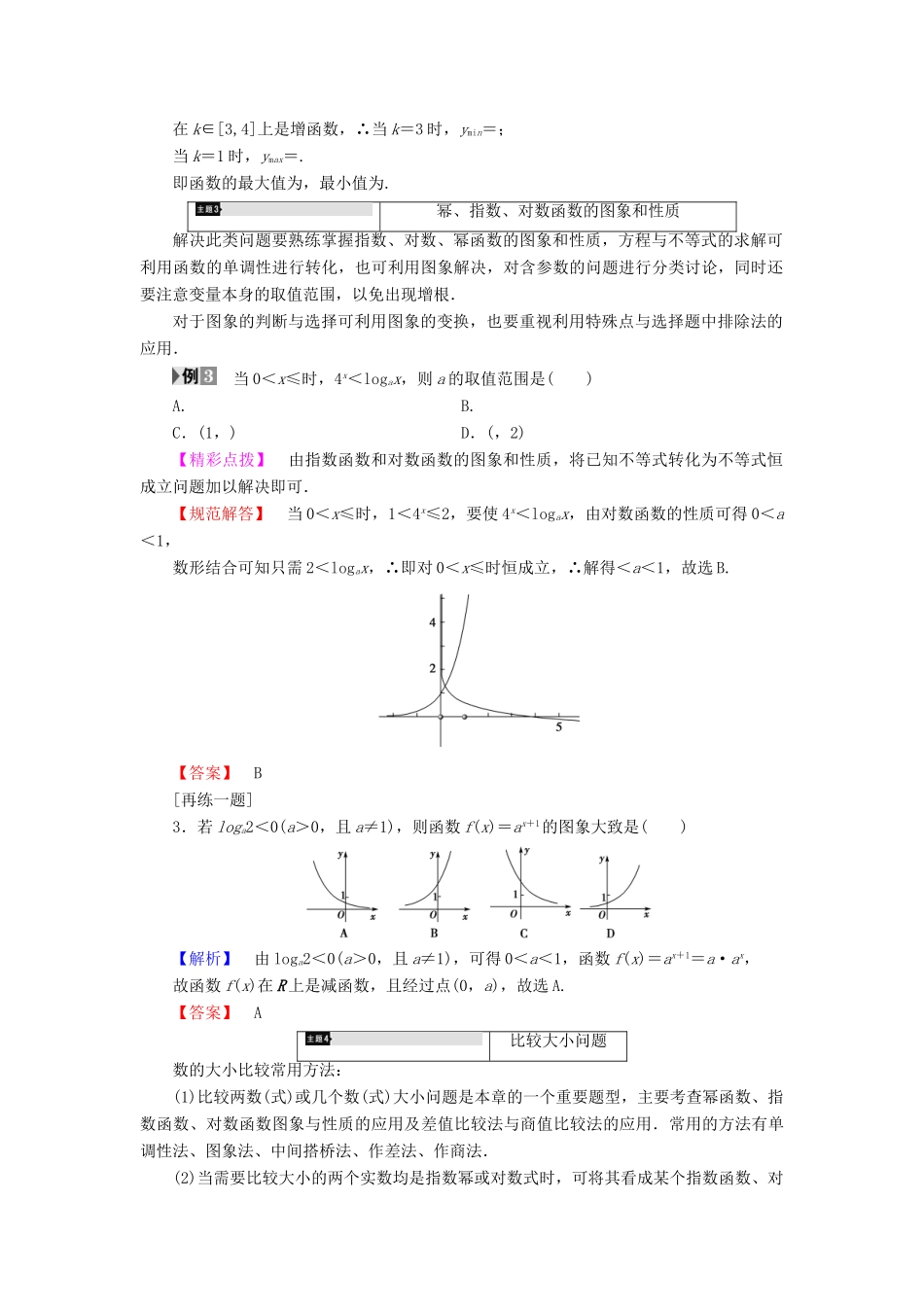
第二章 基本初等函数(Ⅰ)章末分层突破[自我校对]① 分数指数幂② 互为反函数③ 对数函数④y=logax(a>0,且 a≠1)⑤x=logaN(a>0,且 a≠1)⑥y=xα指数、对数的运算解决这类问题首先要熟练掌握指数式、对数式的运算法则,熟练掌握各种变形.如 N=a,ab=N,logaN=b(其中 N >0,a>0,a≠1)是同一数量关系的不同表示形式,因此在许多问题中要能熟练进行它们之间的相互转化,选择适合题目的形式进行运算. 计算:(1)2log32-log3+log38-5log53;(2)0.064--0+[(-2)3]-+16-0.75+0.01.【精彩点拨】 (1)利用对数的运算法则、对数恒等式即可得出;(2)利用指数幂的运算法则即可得出.【规范解答】 (1)原式=log3-3=2-3=-1.(2)原式=0.43×-1+2-4+24×+0.1=-1+++=.[再练一题]1.计算:(1)-0+0.25×-4;(2)log3+2log510+log50.25+71-log72.【解】 (1)原式=-4-1+×()4=-3.(2)原式=log3+log5(100×0.25)+7÷7log72=log33-+log552+=-+2+=.指数、对数型函数的定义域、值域求指数型与对数型函数的定义域主要通过构建不等式(组)来求解,有时解不等式(组)时要借助于指数、对数函数的单调性.涉及指数、对数函数的值域问题有两个类型,一是形如 y=af(x)和 y=logaf(x)的函数,一般要先求 f(x)的值域,然后利用指数、对数的单调性求解;二是形如 y=f(ax)和 y=f(logax)的函数,则要根据 ax和 logax 的范围,利用函数 y=f(x)的性质求解. (1)求函数 y=x2-2x+2(0≤x≤3)的值域;(2)已知-3≤logx≤-,求函数 f(x)=log2·log2的最大值和最小值.【精彩点拨】 (1)令 t=x2-2x+2,则 y=t.根据 x 的范围,求得 t 的范围,可得函数 y=t的范围.(2)由 f(x)=log2·log2=(log2x-1)(log2x-2)=(log2x)2-3log2x+2,结合二次函数的性质即可求解.【规范解答】 (1)令 t=x2-2x+2,则 y=t.又 t=x2-2x+2=(x-1)2+1,0≤x≤3,∴当 x=1 时,tmin=1;当 x=3 时,tmax=5.故 1≤t≤5,∴5≤y≤1,故所求函数的值域为.(2) -3≤logx≤-,∴≤log2x≤3,∴f(x)=log2·log2=(log2x-1)(log2x-2)=(log2x)2-3log2x+2=2-.当 log2x=3 时,f(x)max=2;当 log2x=时,f(x)min=-.[再练一题]2.设 0≤x≤2,y=4x--3·2x+5,试求该函数的最值. 【导学号:97030122】【解】 令 k=2x(0≤x≤2),∴1≤k≤4,则y=22x-1-3·2x+5=k2-3k...