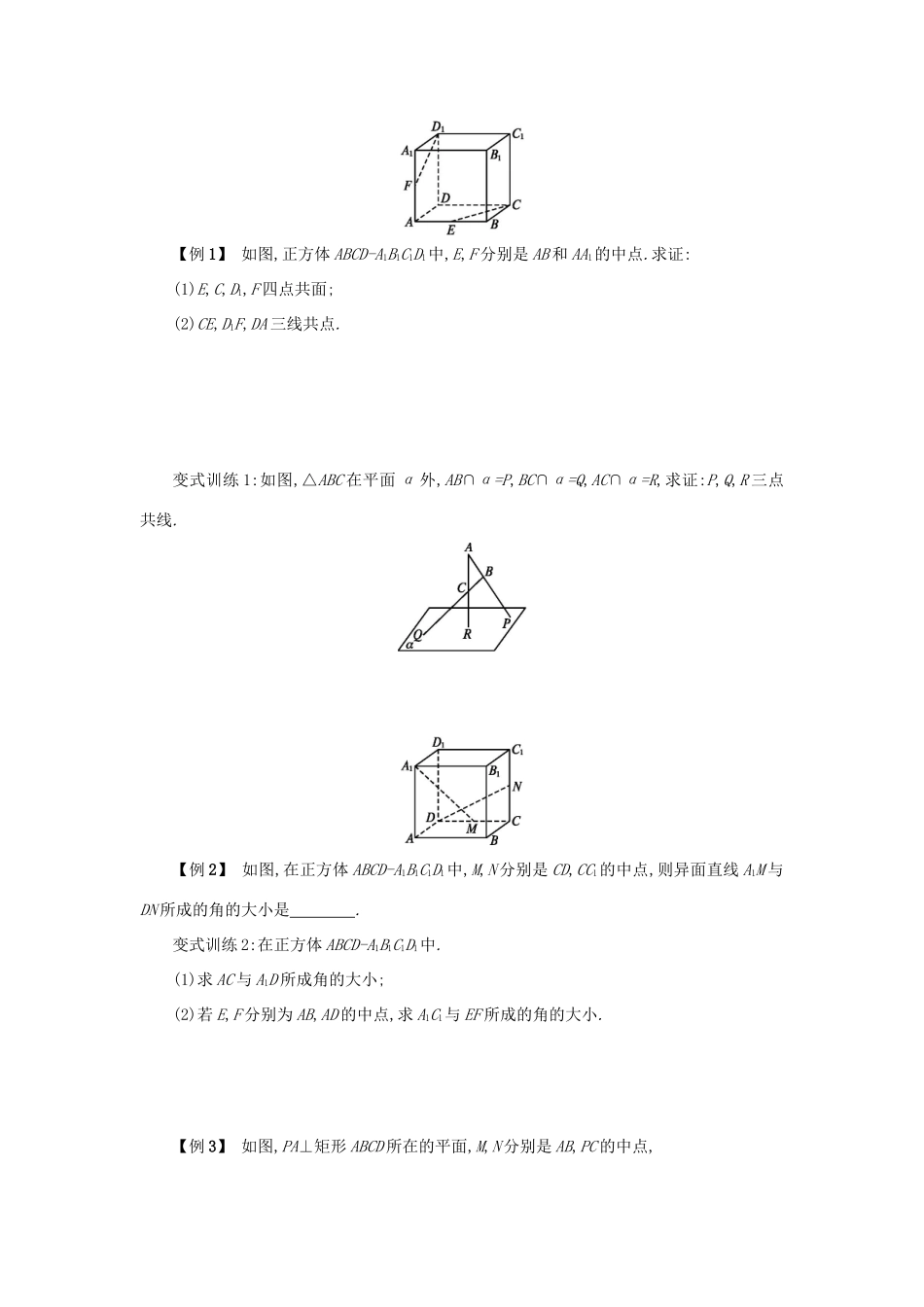
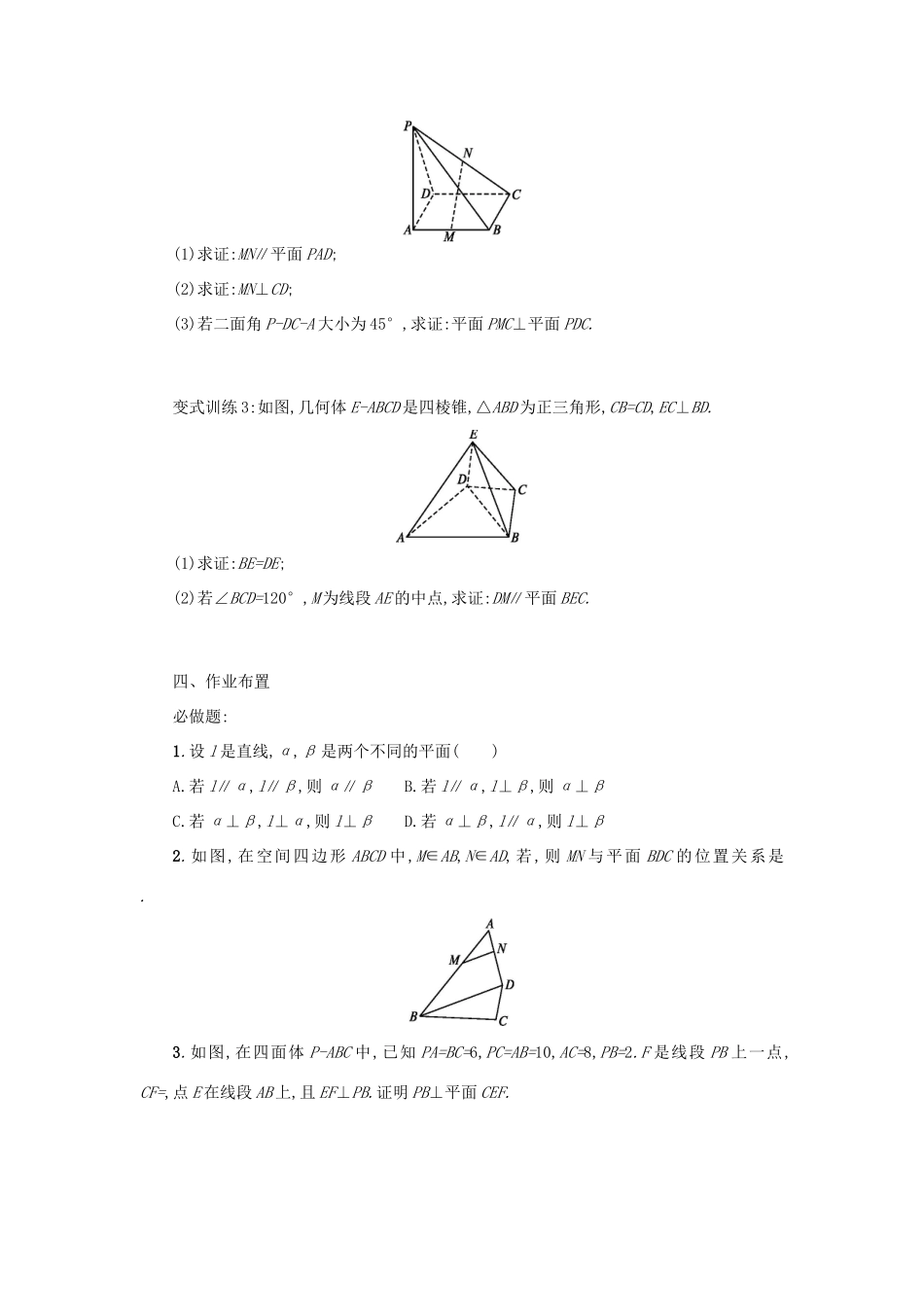
第二章 点、直线、平面之间的位置关系本章小结学习目标重点:空间直线、平面的位置关系,直线、平面平行的判定定理和性质定理,直线、平面垂直的判定定理和性质定理.难点:空间中平行关系、垂直关系、平行与垂直关系之间的转化.合作学习一、知识结构 二、知识梳理 1.四个公理2.直线与直线的位置关系3.等角定理4.直线与平面的位置关系5.平面与平面的位置关系三、【典例选讲】 【例 1】 如图,正方体 ABCD-A1B1C1D1中,E,F 分别是 AB 和 AA1的中点.求证:(1)E,C,D1,F 四点共面;(2)CE,D1F,DA 三线共点.变式训练 1:如图,△ABC 在平面 α 外,AB∩α=P,BC∩α=Q,AC∩α=R,求证:P,Q,R 三点共线.【例 2】 如图,在正方体 ABCD-A1B1C1D1中,M,N 分别是 CD,CC1的中点,则异面直线 A1M 与DN 所成的角的大小是 . 变式训练 2:在正方体 ABCD-A1B1C1D1中.(1)求 AC 与 A1D 所成角的大小;(2)若 E,F 分别为 AB,AD 的中点,求 A1C1与 EF 所成的角的大小.【例 3】 如图,PA⊥矩形 ABCD 所在的平面,M,N 分别是 AB,PC 的中点,(1)求证:MN∥平面 PAD;(2)求证:MN⊥CD;(3)若二面角 P-DC-A 大小为 45°,求证:平面 PMC⊥平面 PDC.变式训练 3:如图,几何体 E-ABCD 是四棱锥,△ABD 为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M 为线段 AE 的中点,求证:DM∥平面 BEC.四、作业布置必做题:1.设 l 是直线,α,β 是两个不同的平面( )A.若 l∥α,l∥β,则 α∥βB.若 l∥α,l⊥β,则 α⊥βC.若 α⊥β,l⊥α,则 l⊥βD.若 α⊥β,l∥α,则 l⊥β2.如图,在空间四边形 ABCD 中,M∈AB,N∈AD,若,则 MN 与平面 BDC 的位置关系是 . 3.如图,在四面体 P-ABC 中,已知 PA=BC=6,PC=AB=10,AC=8,PB=2.F 是线段 PB 上一点,CF=,点 E 在线段 AB 上,且 EF⊥PB.证明 PB⊥平面 CEF.选做题:如图 1,在 Rt△ABC 中,∠C=90°,D,E 分别为 AC,AB 的中点,点 F 为线段 CD 上的一点,将△ADE 沿 DE 折起到△A1DE 的位置,使 A1F⊥CD,如图 2.(1)求证:DE∥平面 A1CB;(2)求证:A1F⊥BE.参考答案二、1.四个公理及推论公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.公理 2:过不在一条直线上的三点,有且只有一个平面.推论 1:经过一条直线和这条直线外一点,有且只有一个平面.推论 2:经过两条相交直线,有且只有一个平面.推论 3:经过两条平行直线,有且只有一个平面.公理 3:如果两...