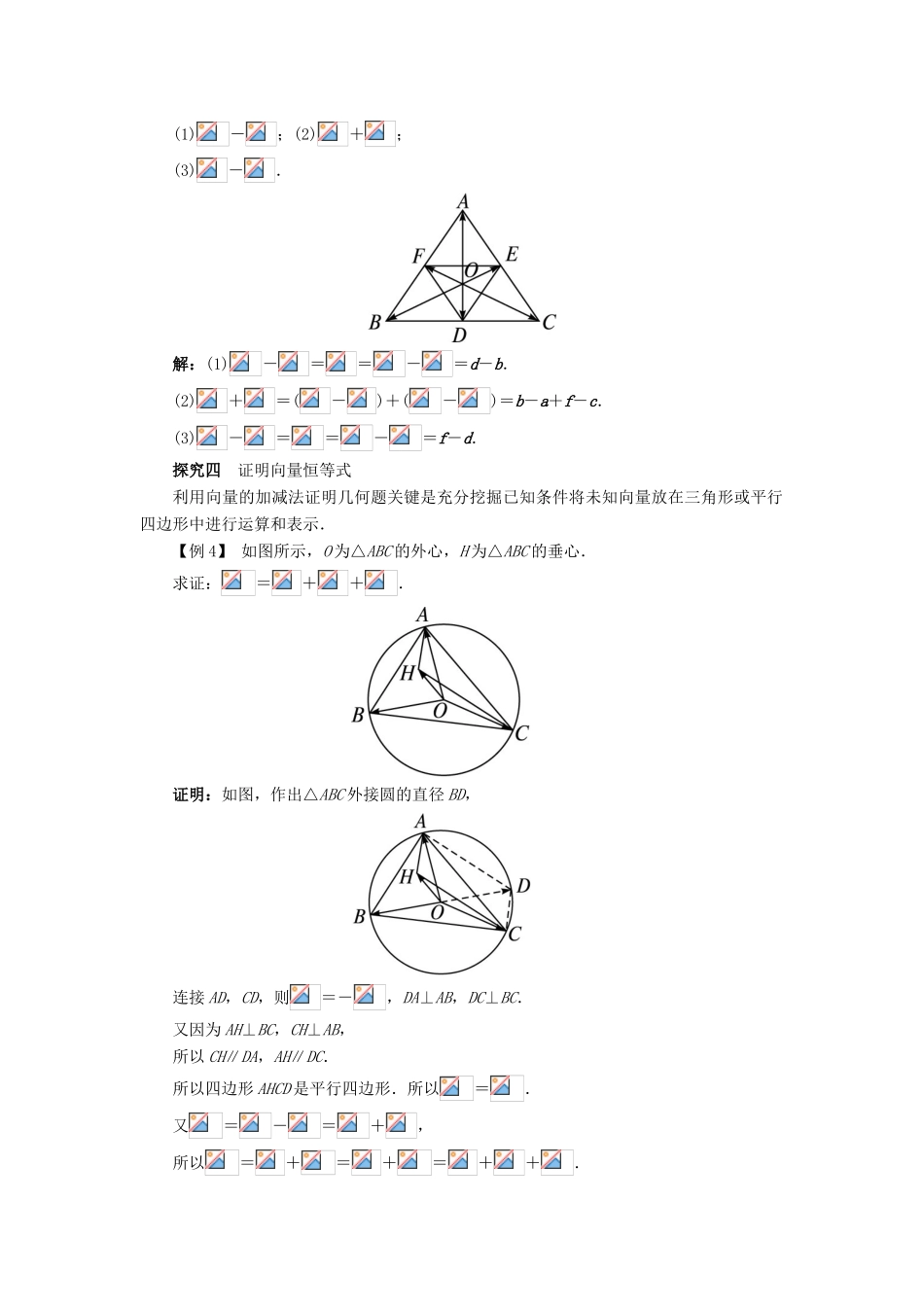
2.1.3 向量的减法课堂探究探究一 向量加减法的几何作图求作向量的和与差要注意三角形法则和平行四边形法则的应用,求作两个向量的差可以转化为两个向量的和来进行,如 a-b,可以作出-b,然后再用加法 a+(-b)即可,也可以直接用向量减法的三角形法则,即把两个向量的始点重合,则两个向量的差向量是连接两个向量的终点,且指向被减向量的终点.【例 1】如图所示,已知向量 a,b,c 不共线,求作向量 a+b-c.分析:首先在平面内选一始点,然后利用向量加法和向量减法的作图法则作图即可(平移向量时要注意向量箭头的方向).解:作法一:在平面内任取一点 O,作=a,=b,图(1)则=a+b,再作=c,则=a+b-c,如图(1)所示.作法二:在平面内任取一点 O,作=a,=b,则=a+b,以 B 点为始点作=-c,则=a+b-c,如图(2)所示.图(2)探究二 化简向量表达式向量的减法运算有如下方法:(1)利用相反向量统一成加法(相当于代数和);(2)运用减法公式-=(正用或逆用均可);(3)辅助点法:利用向量的定义将所有向量转化为以某一确定点为起点的向量,使问题转化为有共同起点的向量问题.另外,应用向量减法的三角形法则需注意“共起点”的条件.【例 2】 化简:(-)-(-)=________.分析:本题主要运用加减法法则进行运算.解:方法 1:(-)-(-)=--+=+++=(+)+(+)=+=0.方法 2:(-)-(-)=--+=(-)+(-)=+=0.方法 3:设 O 为平面内任意一点,则有(-)-(-)=--+=(-)-(-)-(-)+(-)=--+-++-=0.答案:0反思 满足下列两种形式可以化简:(1)首尾相接且为和;(2)起点相同且为差.做题时要注意观察是否有这两种形式,同时要注意逆向应用及统一向量起点方法的应用.探究三 用已知向量表示未知向量用几个基本向量表示某向量的一般步骤是:(1)先观察各个向量在图形中的位置;(2)寻找(或作出)相应的平行四边形或三角形;(3)运用法则找关系;(4)化简结果.【例 3】 如图,已知=a,=b,=c,=d,=e,=f,试用 a,b,c,d,e,f 表示:(1)-;(2)+;(3)-.解:(1)-==-=d-b.(2)+=(-)+(-)=b-a+f-c.(3)-==-=f-d.探究四 证明向量恒等式利用向量的加减法证明几何题关键是充分挖掘已知条件将未知向量放在三角形或平行四边形中进行运算和表示.【例 4】 如图所示,O 为△ABC 的外心,H 为△ABC 的垂心.求证:=++.证明:如图,作出△ABC 外接圆的...