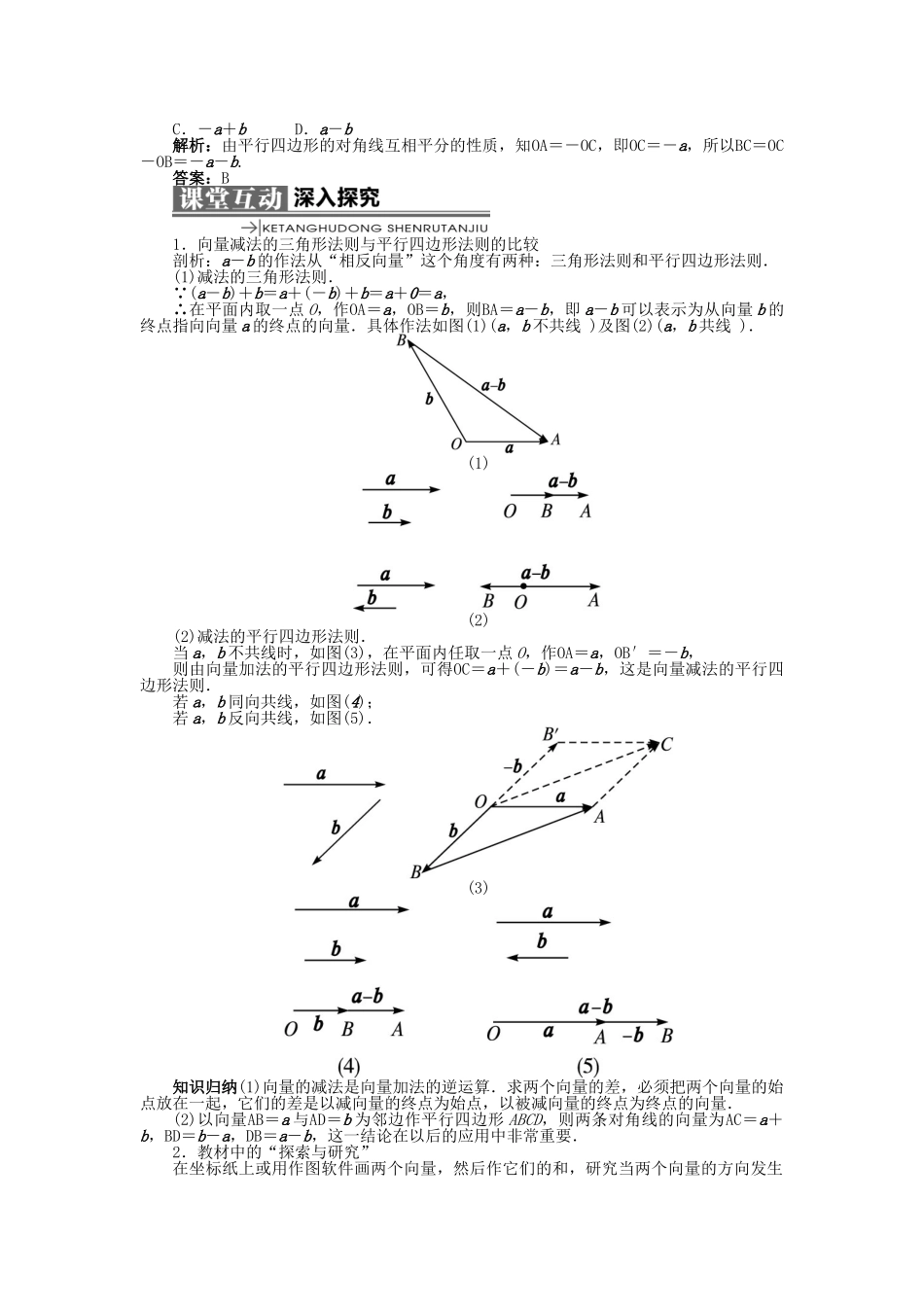
2.1.3 向量的减法基础知识基本能力1.掌握向量的减法运算,并理解其几何意义.(重点、难点)2.理解向量的相反向量的意义,从而加深对向量减法的本质特征的领悟.(重点)1.能将向量的减法运算转化为向量的加法运算.(难点)2.理解数的减法与向量的减法的联系与区别.(易混点)1.向量减法的定义(1)已知向量 a,b(如图),作OA=a,OB=b,则 b+BA=a,向量BA叫做向量 a 与 b 的差,并记作 a-b,即BA=a-b=OA-OB.(2)如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点为始点,被减向量的终点为终点的向量.(3)一个向量BA等于它的终点相对于点 O 的位置向量OA减去它的始点相对于点 O 的位置向量OB,或简记“终点向量减始点向量”.【自主测试 1】如图所示,在▱ABCD 中,AB=a,AD=b,则用 a,b 表示向量BD是( )A.a-b B.b-a C.b+2a D.b+a答案:B2.相反向量的定义和性质及向量减法的再理解(1)定义.与向量 a 方向相反且等长的向量叫做 a 的相反向量,记作-a(如图所示).(2)性质.①a+(-a)=(-a)+a=0;②-(-a)=a;③ 零向量的相反向量仍是 0,即 0=-0.(3)向量减法的再理解.从一个向量减去另一个向量等于加上这个向量的相反向量.因此关于向量减法的作图,一是利用向量减法的定义直接作图,二是利用相反向量作图.相反向量和相反数一样吗?答:相反向量与相反数是不一样的,相反数是两个数的符号相反,大小相等;相反向量则是两个向量的方向相反,大小相等.【自主测试 2】若平行四边形 ABCD 的对角线 AC 和 BD 相交于点 O,且OA=a,OB=b,用 a,b 表示向量BC为( )A.a+b B.-a-bC.-a+b D.a-b解析:由平行四边形的对角线互相平分的性质,知OA=-OC,即OC=-a,所以BC=OC-OB=-a-b.答案:B1.向量减法的三角形法则与平行四边形法则的比较剖析:a-b 的作法从“相反向量”这个角度有两种:三角形法则和平行四边形法则.(1)减法的三角形法则. (a-b)+b=a+(-b)+b=a+0=a,∴在平面内取一点 O,作OA=a,OB=b,则BA=a-b,即 a-b 可以表示为从向量 b 的终点指向向量 a 的终点的向量.具体作法如图(1)(a,b 不共线 )及图(2)(a,b 共线 ).(1)(2)(2)减法的平行四边形法则.当 a,b 不共线时,如图(3),在平面内任取一点 O,作OA=a,OB′=-b,则由向量加法的平行四边形法则,可得OC=a+(-b)=a-b,这是向量减法的平行四边形法...