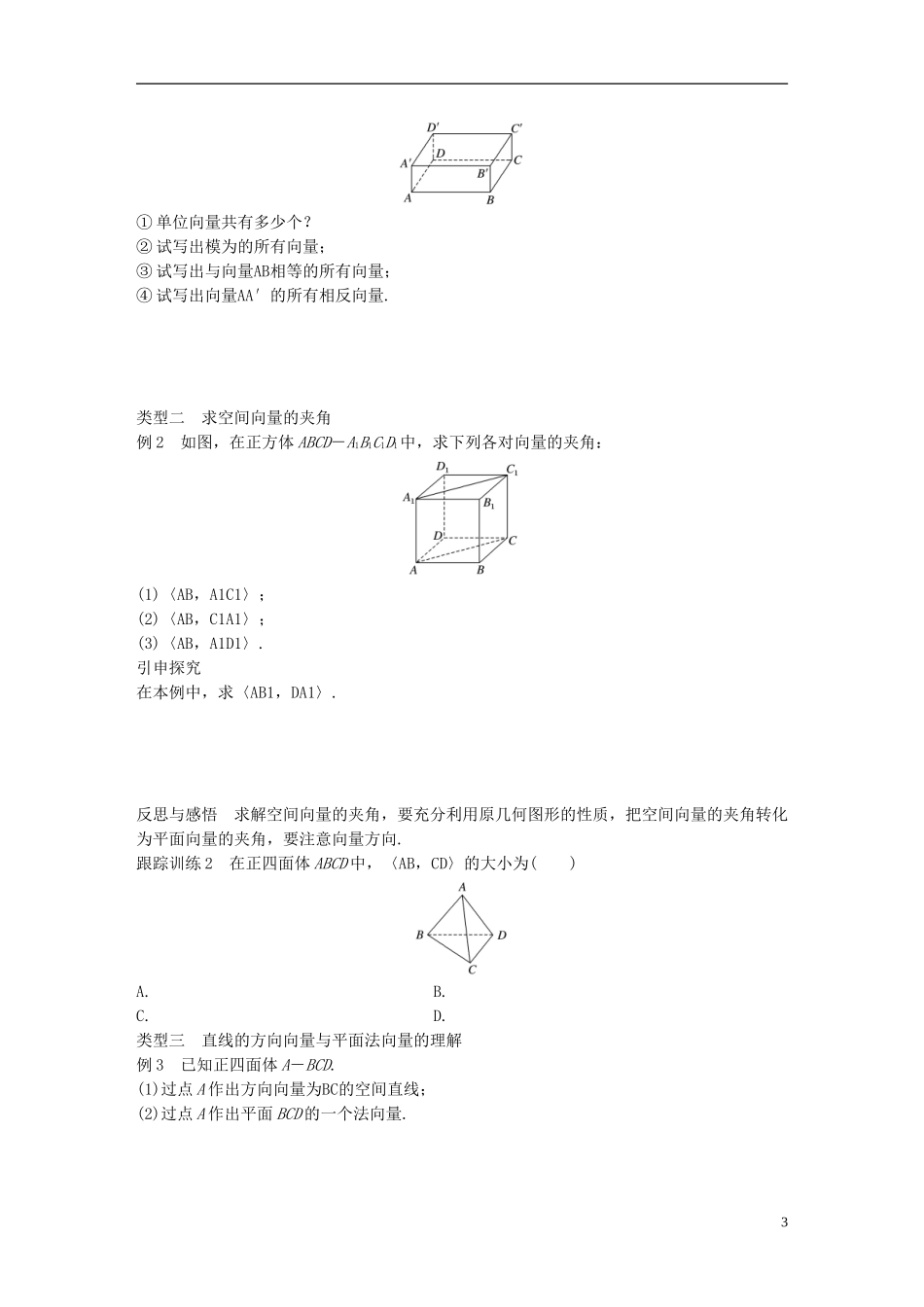
1 从平面向量到空间向量学习目标 1.理解空间向量的概念.2.了解空间向量的表示法,了解自由向量的概念.3.理解空间向量的夹角.4.理解直线的方向向量与平面的法向量的概念.知识点一 空间向量的概念思考 1 类比平面向量的概念,给出空间向量的概念.思考 2 若表示两个相等空间向量的有向线段的起点相同,则终点也一定相同吗?梳理 空间向量的有关概念(1)定义:在空间中,把既有______又有______的量,叫作空间向量.(2)长度:空间向量的大小叫作向量的______或____.(3)表示法(4)自由向量:与向量的起点无关的向量.知识点二 空间向量的夹角思考 在平面内,若非零向量 a 与 b 共线,则它们的夹角是多少?梳理 空间向量的夹角(1)文字叙述:a,b 是空间中两个非零向量,过空间任意一点 O,作OA=a,OB=b,则________叫作向量 a 与向量 b 的夹角,记作______________.(2)图形表示:角度表示〈a,b〉=____〈a,b〉是____〈a,b〉是____〈a,b〉是____〈a,b〉=____1(3)范围:____≤〈a,b〉≤____.(4)空间向量的垂直:如果〈a,b〉=______,那么称 a 与 b 互相垂直,记作________.知识点三 向量与直线、平面1.向量与直线与平面向量一样,也可用空间向量描述空间直线的方向.如图所示.l 是空间一直线,A,B 是直线 l 上任意两点,则称AB为直线 l 的______向量,显然,与AB平行的任意非零向量 a 也是直线 l 的方向向量,直线的方向向量______于该直线.2.向量与平面如图,如果直线 l 垂直于平面 α,那么把直线 l 的方向向量 a 叫作平面 α 的________.类型一 有关空间向量的概念的理解例 1 给出以下结论:① 两个空间向量相等,则它们的起点和终点分别相同;②若空间向量 a,b 满足|a|=|b|,则 a=b;③在正方体 ABCD-A1B1C1D1中,必有AC=A1C1;④若空间向量 m,n,p 满足 m=n,n=p,则 m=p.其中不正确的个数是( )A.1 B.2 C.3 D.4反思与感悟 在空间中,向量、向量的模、相等向量的概念和在平面中向量的相关概念完全一致,两向量相等的充要条件是两个向量的方向相同,模相等.两向量互为相反向量的充要条件是大小相等,方向相反.跟踪训练 1 (1)在平行六面体 ABCD—A1B1C1D1中,下列四对向量:①AB与C1D1;②AC1与BD1;③AD1与C1B;④A1D与B1C.其中互为相反向量的有 n 对,则 n 等于( ) A.1 B.2C.3 D.4(2)如图,在长方体 ABCD-A′B′C′D′中,AB=3,AD=2,AA′=1,则分别...