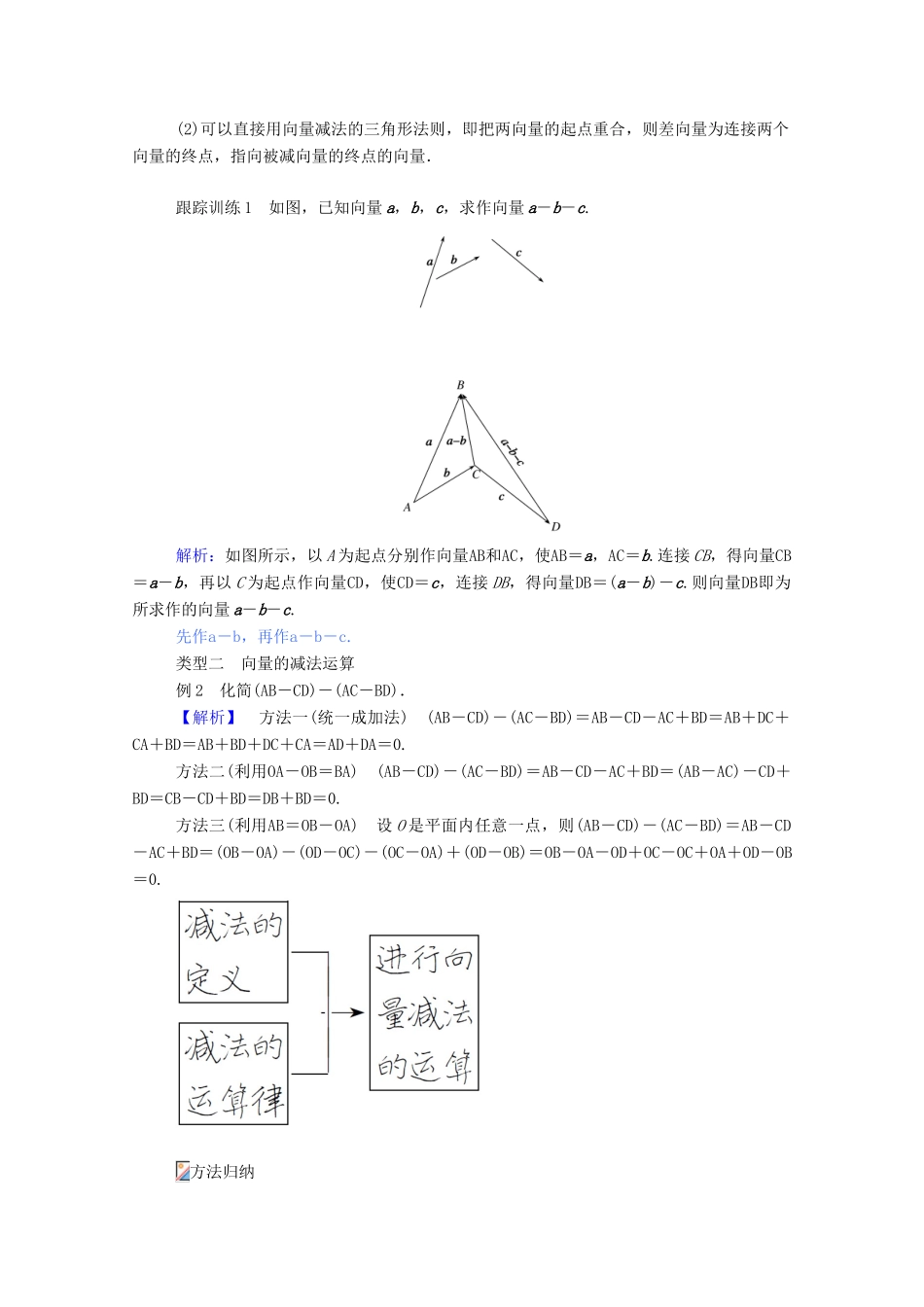
第 2 课时 向量减法运算及其几何意义1.相反向量与 a 长度相等,方向相反的向量,叫作 a 的相反向量,记作-a.(1)零向量的相反向量仍是零向量,即-0=0.(2)任一向量与其相反向量的和是零向量,即 a+(-a)=0.(3)如果 a,b 是互为相反的向量,则 a=-b,b=-a,a+b=0.2.向量的减法(1)定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量.(2)几何意义:已知 a,b,在平面内任取一点 O,作OA=a,OB=b,则BA=a-b,即 a-b 可以表示为从向量 b 的终点指向向量 a 的终点的向量. 1.准确理解向量减法的几何意义(1)向量减法是向量加法的逆运算.设x+b=a,则x=a-b,如图,设OA =a,OB =b.由向量加法的三角形法则可知OA =OB +BA,∴BA =OA -OB =a-b.(2)对于两个共起点的向量,它们的差就是连接这两个向量的终点,方向指向被减的向量.(3)以向量AB=a,AD=b为邻边作平行四边形 ABCD,则两条对角线的向量为AC=a+b,BD =b-a,DB =a-b.2.若a,b是不共线向量,|a+b|与|a-b|的几何意义比较,如图所示,设OA=a,OB=b.根据向量加法的平行四边形法则和向量减法的三角形法则,有OC=a+b,BA=a-b.因为四边形 OACB 是平行四边形,所以|a+b|=|OC|,|a-b|=|BA|分别是以 OA,OB 为邻边的平行四边形的两条对角线的长.[小试身手]1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)(1)两向量首尾相连,和向量由第一个向量的始点指向第二个向量的终点.( )(2)向量 a-b 当它们起点重合时可以看作从向量 b 的终点指向向量 a 的终点的向量.( )(3)向量加法的运算律同样适用于向量的减法运算.( )答案:(1)√ (2)√ (3)√2.非零向量 m 与 n 是相反向量,下列不正确的是( )A.m=n B.m=-nC.|m|=|n| D.方向相反解析:零向量 m 与 n 是相反向量,则有 m=-n,|m|=|n|.答案:A3.在三角形 ABC 中,BC=a,CA=b,则AB=( )A.a-b B.b-aC.a+b D.-a-b解析:AB=CB-CA=-BC-CA=-a-b.答案:D4.PA-PB=________.解析:PA-PB=BA.答案:BA类型一 已知向量作差向量例 1 如图,已知向量 a,b,c 不共线,求作向量 a+b-c.【解析】 方法一 如图①,在平面内任取一点 O,作OA=a,OB=b,OC=c,连接BC,则CB=b-c.过点 A 作 AD 綊 BC,连接 OD,则AD=b-c,所以OD=OA+AD=a+b-c.方法二 如图②,在平面内任...