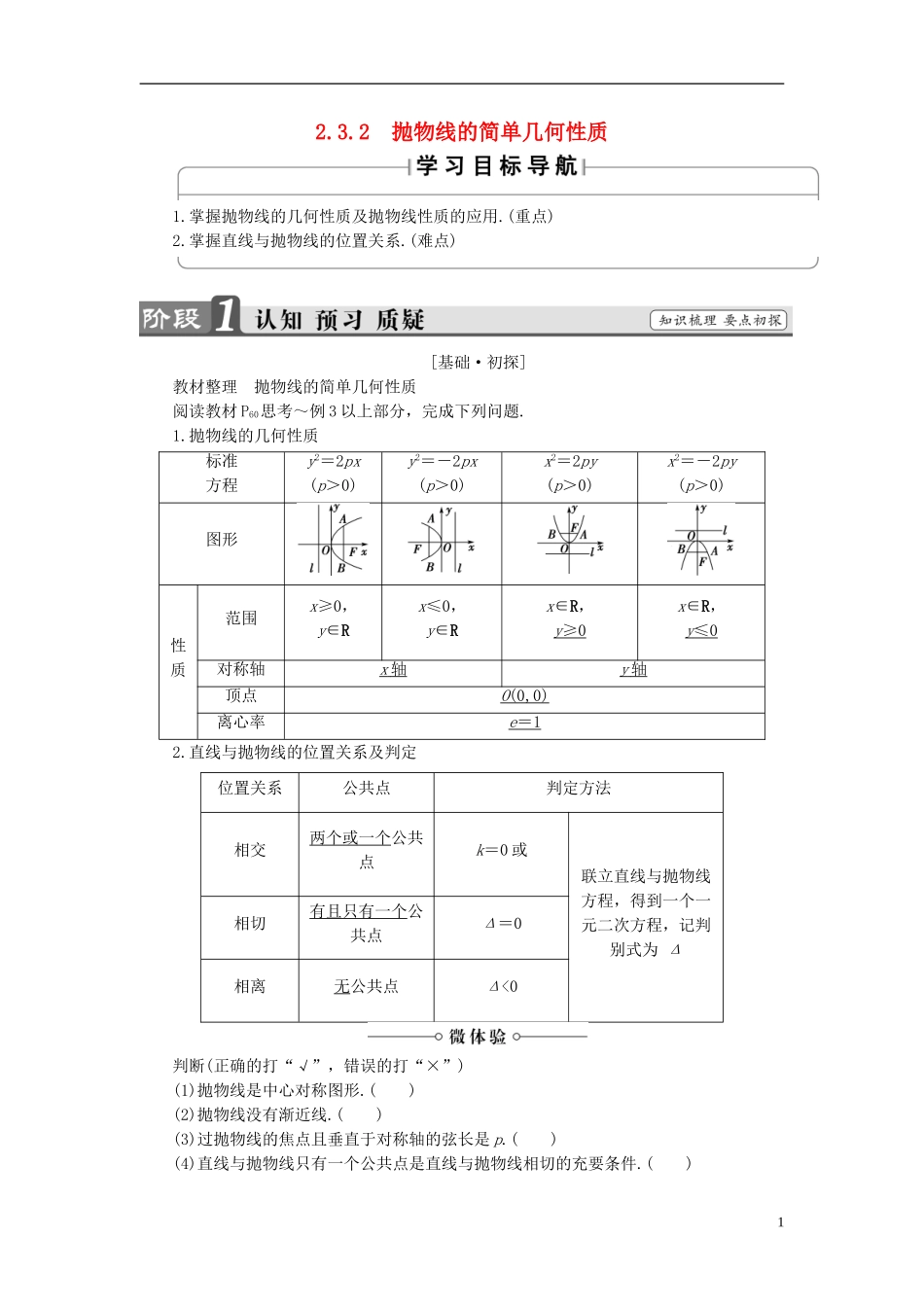
2.3.2 抛物线的简单几何性质1.掌握抛物线的几何性质及抛物线性质的应用.(重点)2.掌握直线与抛物线的位置关系.(难点)[基础·初探]教材整理 抛物线的简单几何性质阅读教材 P60思考~例 3 以上部分,完成下列问题.1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形性质范围x≥0,y∈Rx≤0,y∈Rx∈R,y ≥0 x∈R,y ≤0 对称轴x 轴 y 轴 顶点O (0,0) 离心率e = 1 2.直线与抛物线的位置关系及判定位置关系公共点判定方法相交两个或一个公共点k=0 或联立直线与抛物线方程,得到一个一元二次方程,记判别式为 Δ相切有且只有一个公共点Δ=0相离无公共点Δ<0判断(正确的打“√”,错误的打“×”)(1)抛物线是中心对称图形.( )(2)抛物线没有渐近线.( )(3)过抛物线的焦点且垂直于对称轴的弦长是 p.( )(4)直线与抛物线只有一个公共点是直线与抛物线相切的充要条件.( )1【答案】 (1)× (2)√ (3)× (4)×[小组合作型]抛物线的几何性质 (1)抛物线顶点在坐标原点,以 y 轴为对称轴,过焦点且与 y 轴垂直的弦长为16,则抛物线方程为________.【自主解答】 因为过焦点且与对称轴 y 轴垂直的弦长等于 p 的 2 倍,所以 2p=16.故所求抛物线方程为 x2=±16y.【答案】 x2=±16y(2)已知抛物线的方程为 y=ax2(a≠0),求该抛物线的焦点坐标和准线方程. 【导学号:97792029】【自主解答】 抛物线方程 y=ax2(a≠0)可化为 x2=y(a≠0).当 a>0 时,抛物线开口向上,焦点坐标为,准线方程为 y=-.当 a<0 时,抛物线开口向下,焦点坐标为,准线方程为 y=-.综上所述,抛物线 y=ax2(a≠0)的焦点坐标为,准线方程为 y=-.把握三个要点确定抛物线简单几何性质1.开口:由抛物线标准方程看图象开口,关键是看准二次项是 x 还是 y,一次项的系数是正还是负.2.关系:顶点位于焦点与准线中间、准线垂直于对称轴.3.定值:焦点到准线的距离为 p;过焦点垂直于对称轴的弦(又称为通径)长为 2p;离心率恒等于 1.[再练一题]1.抛物线的顶点在原点,对称轴重合于椭圆 9x2+4y2=36 短轴所在的直线,抛物线焦点到顶点的距离为 3,求抛物线的方程及抛物线的准线方程.【解】 椭圆的方程可化为+=1,其短轴在 x 轴上,∴抛物线的对称轴为 x 轴,∴设抛物线的方程为 y2=2px 或 y2=-2px(p>0). 抛物线的焦点到顶点的距离为 3,即=3,∴p=6.∴抛物线的标准方...