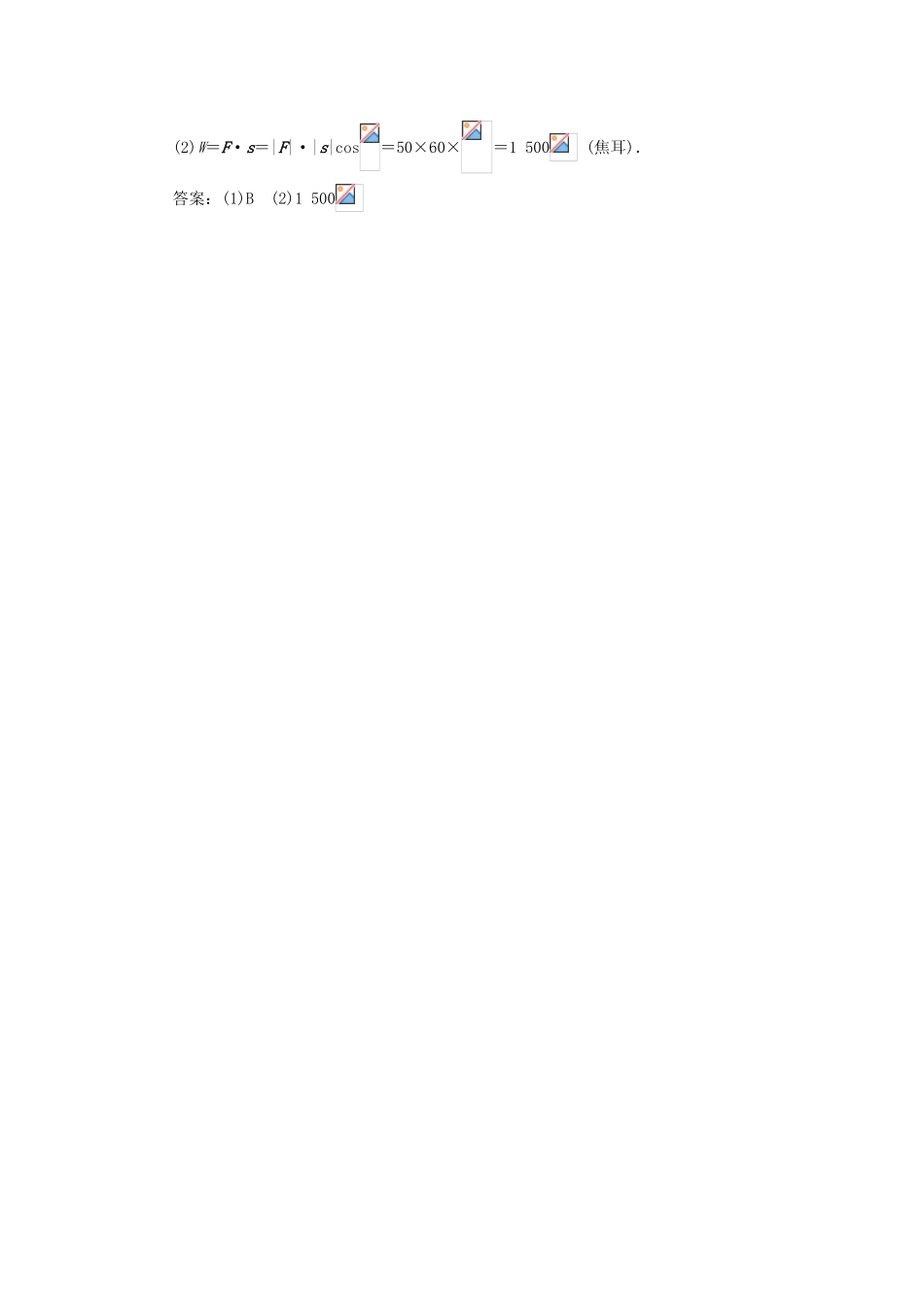
2.5 平面向量应用举例(第 2 课时)课堂探究探究一用向量法解决速度问题运用向量解决物理中的速度问题时,一般涉及速度的合成与分解,充分借助向量三角形法则把物理问题抽象转化为数学问题,同时正确作图是前提.【典型例题 1】 在风速为 75(-) km/h 的西风中,飞机以 150 km/h 的航速向西北方向飞行,求没有风时飞机的航速和航向.思路分析:解本题首先根据题意作图,再把物理问题转化为向量的有关运算求解.解:设 ω=风速,va=有风时飞机的航行速度,vb=无风时飞机的航行速度,vb=va-ω.如图所示.设||=|va|,||=|ω|,||=|vb|,作 AD∥BC,CD⊥AD 于 D,BE⊥AD 于 E,则∠BAD=45°.设||=150,则||=75(-).∴||=||=||=75,||=75.从而||=150,∠CAD=30°.∴|vb|=150 km/h,方向为北偏西 60°.探究二 用向量解决力学问题1.在解决物理问题时,把物理中的矢量抽象成向量,然后在三角形或平行四边形中求解.2.用向量方法解决物理问题的步骤:一是把物理问题中的相关量用向量表示;二是转化为向量问题的模型,通过向量运算解决问题;三是将结果还原.【典型例题 2】 (1)两个大小相等的共点力 F1,F2,当它们的夹角为 90°时,合力的大小为 20 N,则当它们的夹角为 120°时,合力的大小为( )A.40 N B.10 NC.20 N D. N(2)一纤夫用纤绳拉船沿直线方向前进 60 m,若纤绳与行进的方向夹角为,此人的拉力为 50 N,则纤夫对船所做的功为__________焦耳.解析:(1)对于两个大小相等的共点力 F1,F2,当它们的夹角为 90°,合力的大小为20 N 时,由三角形法则可知,这两个力的大小都是 10 N;当它们的夹角为 120°时,由三角形法则可知力的合成构成一个等边三角形,因此合力的大小为 10 N.(2)W=F·s=|F|·|s|cos=50×60×=1 500 (焦耳).答案:(1)B (2)1 500