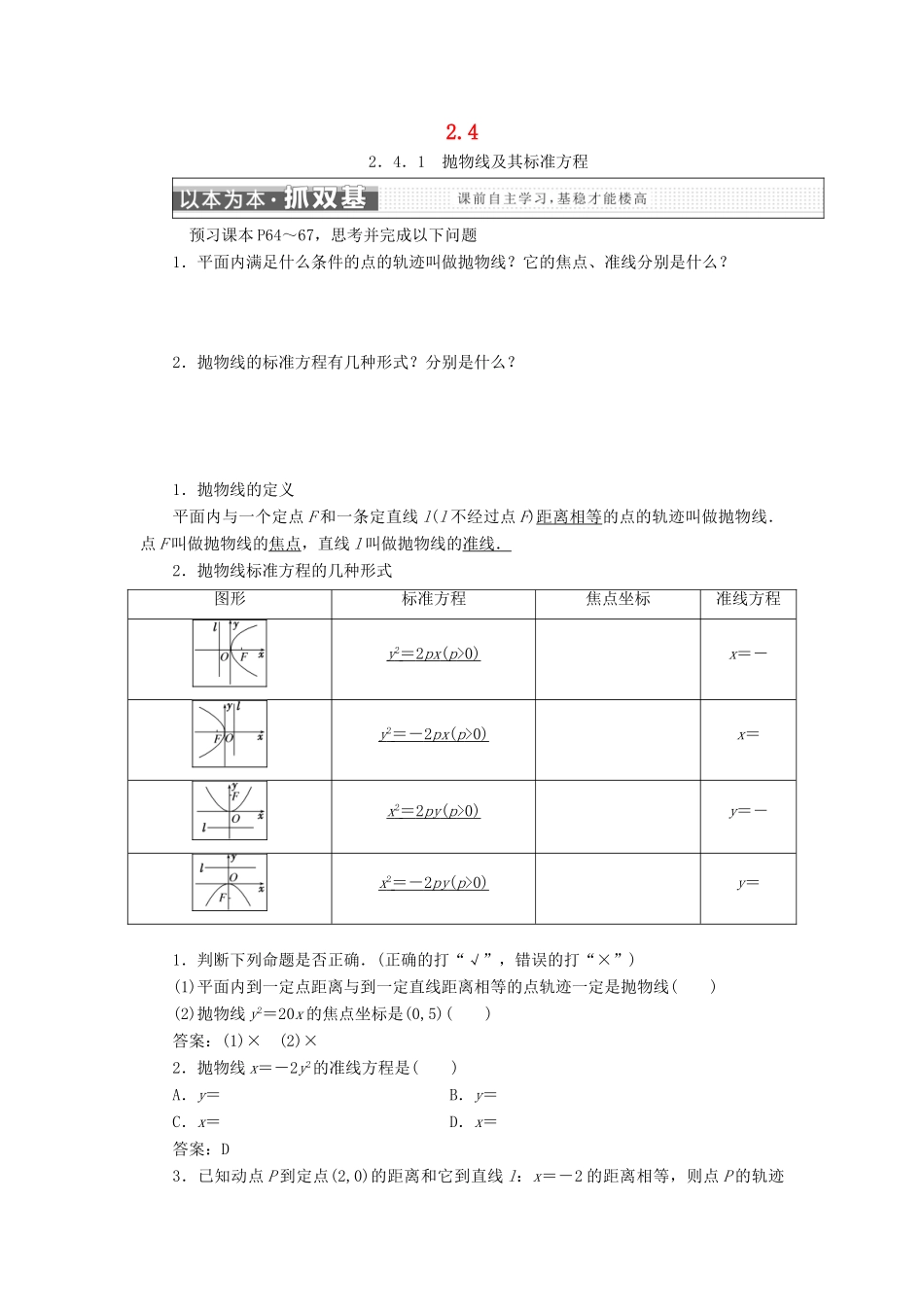
2.4 2.4.1 抛物线及其标准方程 预习课本 P64~67,思考并完成以下问题1.平面内满足什么条件的点的轨迹叫做抛物线?它的焦点、准线分别是什么? 2.抛物线的标准方程有几种形式?分别是什么? 1.抛物线的定义平面内与一个定点 F 和一条定直线 l(l 不经过点 F)距离相等的点的轨迹叫做抛物线.点 F 叫做抛物线的焦点,直线 l 叫做抛物线的准线.2.抛物线标准方程的几种形式图形标准方程焦点坐标准线方程y 2 = 2 px ( p >0) x=-y 2 =- 2 px ( p >0) x=x 2 = 2 py ( p >0) y=-x 2 =- 2 py ( p >0) y=1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)平面内到一定点距离与到一定直线距离相等的点轨迹一定是抛物线( )(2)抛物线 y2=20x 的焦点坐标是(0,5)( )答案:(1)× (2)×2.抛物线 x=-2y2的准线方程是( )A.y= B.y=C.x= D.x=答案:D3.已知动点 P 到定点(2,0)的距离和它到直线 l:x=-2 的距离相等,则点 P 的轨迹方程为________.答案:y2=8x求抛物线的标准方程[典例] 求适合下列条件的抛物线的标准方程:(1)过点 M(-6,6);(2)焦点 F 在直线 l:3x-2y-6=0 上.[解] (1)由于点 M(-6,6)在第二象限,∴过 M 的抛物线开口向左或开口向上.若抛物线开口向左,焦点在 x 轴上,设其方程为 y2=-2px(p>0),将点 M(-6,6)代入,可得 36=-2p×(-6),∴p=3.∴抛物线的方程为 y2=-6x.若抛物线开口向上,焦点在 y 轴上,设其方程为 x2=2py(p>0),将点 M(-6,6)代入可得,36=2p×6,∴p=3,∴抛物线的方程为 x2=6y.综上所述,抛物线的标准方程为 y2=-6x 或 x2=6y.(2)① 直线 l 与 x 轴的交点为(2,0),∴抛物线的焦点是 F(2,0),∴=2,∴p=4,∴抛物线的标准方程是 y2=8x.② 直线 l 与 y 轴的交点为(0,-3),即抛物线的焦点是 F(0,-3),∴=3,∴p=6,∴抛物线的标准方程是 x2=-12y.综上所述,所求抛物线的标准方程是 y2=8x 或 x2=-12y.求抛物线的标准方程的关键与方法(1)关键:确定焦点在哪条坐标轴上,进而求方程的有关参数.(2)方法:①直接法,建立恰当坐标系,利用抛物线的定义列出动点满足的条件,列出对应方程,化简方程.② 直接根据定义求 p,最后写标准方程.③ 利用待定系数法设标准方程,找有关的方程组求系数. [活学活用] 求下列抛物线的焦点坐标和...