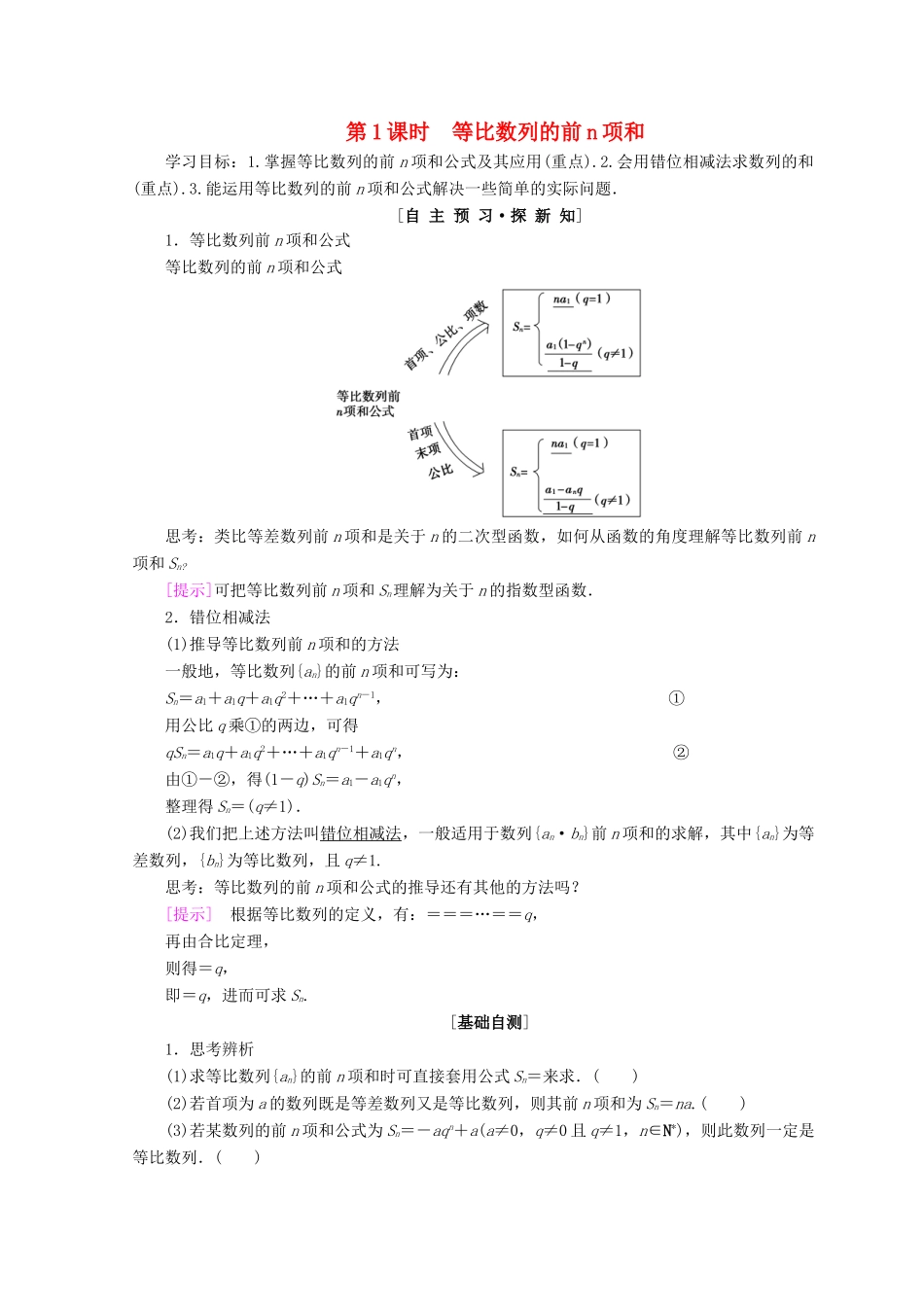
第 1 课时 等比数列的前 n 项和学习目标:1.掌握等比数列的前 n 项和公式及其应用(重点).2.会用错位相减法求数列的和(重点).3.能运用等比数列的前 n 项和公式解决一些简单的实际问题.[自 主 预 习·探 新 知]1.等比数列前 n 项和公式等比数列的前 n 项和公式思考:类比等差数列前 n 项和是关于 n 的二次型函数,如何从函数的角度理解等比数列前 n项和 Sn?[提示]可把等比数列前 n 项和 Sn理解为关于 n 的指数型函数.2.错位相减法(1)推导等比数列前 n 项和的方法一般地,等比数列{an}的前 n 项和可写为:Sn=a1+a1q+a1q2+…+a1qn-1, ①用公比 q 乘①的两边,可得qSn=a1q+a1q2+…+a1qn-1+a1qn, ②由①-②,得(1-q)Sn=a1-a1qn,整理得 Sn=(q≠1).(2)我们把上述方法叫错位相减法,一般适用于数列{an·bn}前 n 项和的求解,其中{an}为等差数列,{bn}为等比数列,且 q≠1.思考:等比数列的前 n 项和公式的推导还有其他的方法吗?[提示] 根据等比数列的定义,有:===…==q,再由合比定理,则得=q,即=q,进而可求 Sn.[基础自测]1.思考辨析(1)求等比数列{an}的前 n 项和时可直接套用公式 Sn=来求.( )(2)若首项为 a 的数列既是等差数列又是等比数列,则其前 n 项和为 Sn=na.( )(3)若某数列的前 n 项和公式为 Sn=-aqn+a(a≠0,q≠0 且 q≠1,n∈N*),则此数列一定是等比数列.( )[答案] (1)× (2)√ (3)√ 提示:(1)错误.在求等比数列前 n 项和时,首先应看公比 q 是否为 1,若 q≠1,可直接套用,否则应讨论求和.(2)正确.若数列既是等差数列,又是等比数列,则是非零常数列,所以前 n 项和为 Sn=na.(3)正确.根据等比数列前 n 项和公式 Sn=(q≠0 且 q≠1)变形为 Sn=-qn(q≠0 且 q≠1),若令 a=,则和式可变形为 Sn=a-aqn.2.等比数列{an}中,a1=1,q=2,则 S5=________.31 [S5===31.]3.数列,,,…的前 10 项的和 S10=________.【导学号:91432215】 [S10=+++…+,则 S10=++…++.两式相减得,S10=+++…+-=-,所以 S10=.]4.某厂去年产值为 a,计划在 5 年内每年比上一年的产值增长 10%,从今年起 5 年内,该厂的总产值为________.11(1.15 - 1)a [ 去 年 产 值 为 a , 从 今 年 起 5 年 内 各 年 的 产 值 分 别 为1.1a,1.12a,1.13a,1.14a,1.15...