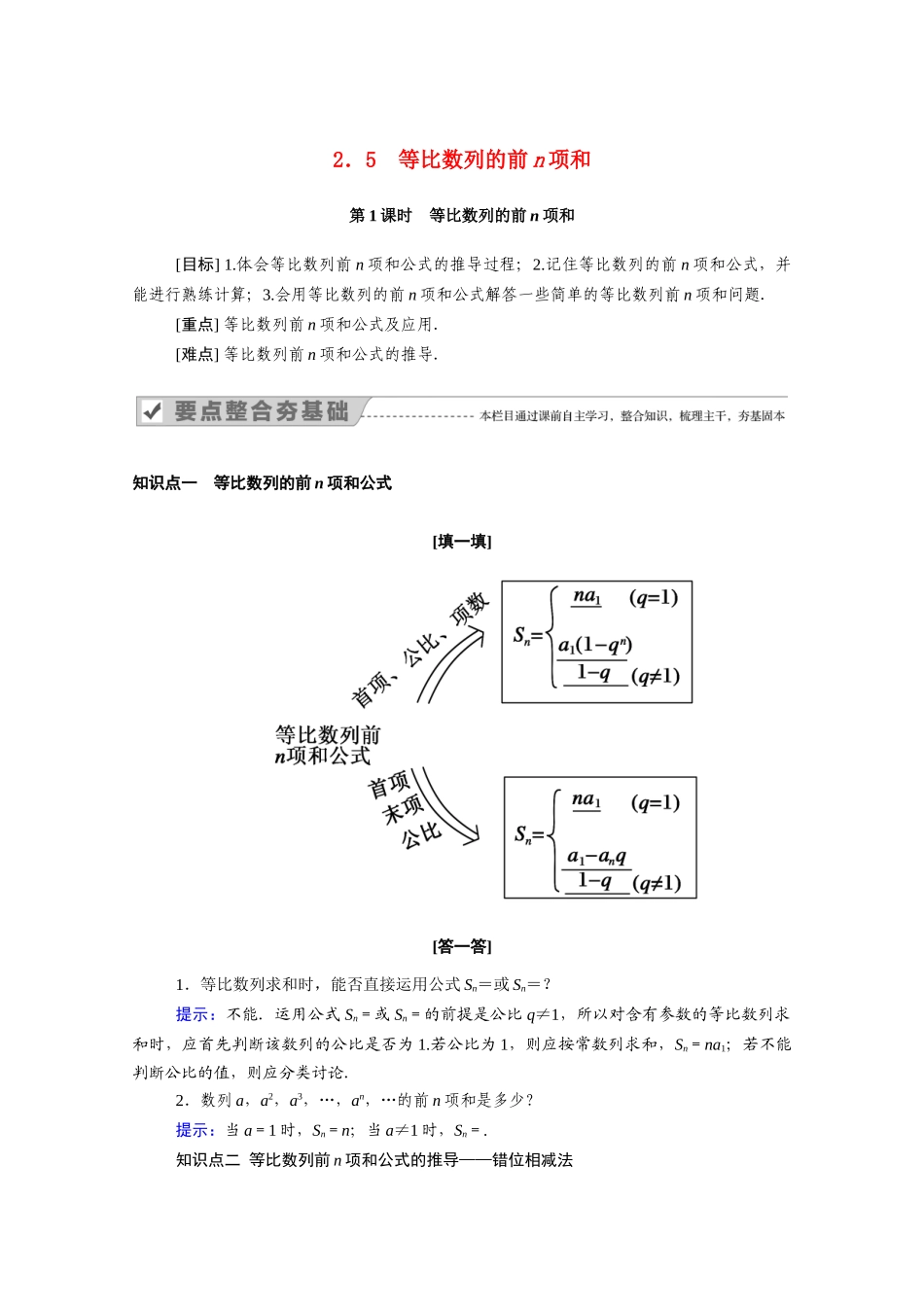
2.5 等比数列的前 n 项和第 1 课时 等比数列的前 n 项和[目标] 1.体会等比数列前 n 项和公式的推导过程;2.记住等比数列的前 n 项和公式,并能进行熟练计算;3.会用等比数列的前 n 项和公式解答一些简单的等比数列前 n 项和问题.[重点] 等比数列前 n 项和公式及应用.[难点] 等比数列前 n 项和公式的推导.知识点一 等比数列的前 n 项和公式 [填一填][答一答]1.等比数列求和时,能否直接运用公式 Sn=或 Sn=?提示:不能.运用公式 Sn=或 Sn=的前提是公比 q≠1,所以对含有参数的等比数列求和时,应首先判断该数列的公比是否为 1.若公比为 1,则应按常数列求和,Sn=na1;若不能判断公比的值,则应分类讨论.2.数列 a,a2,a3,…,an,…的前 n 项和是多少?提示:当 a=1 时,Sn=n;当 a≠1 时,Sn=.知识点二 等比数列前 n 项和公式的推导——错位相减法 [填一填]一般地,对于等比数列 a1,a2,a3,…,an,…,它的前 n 项和是 Sn=a1+a2+a3+…+an.根据等比数列的通项公式,上式可写成 Sn=a1+a1q+a1q2+…+a1qn-2+a1qn-1 ①,① 的两边同乘以 q,得 qSn=a1q + a 1q 2 + a 1q 3 + … + a 1q n - 1 + a 1q n ②,用①的两边分别减去②的两边,得(1-q)Sn=a1- a 1q n .当 q≠1 时,等比数列的前 n 项和公式为 Sn=.因为 a1qn=(a1qn-1)q=anq,所以上面的公式还可以写成 Sn=.当 q=1 时,数列{an}即为常数列 a1,a1,a1,…,a1,…,易得它的前 n 项和 Sn=na1.[答一答]3.“错位相减法”适用于什么样的数列求和?提示:它适用于求一个等差数列与一个等比数列的积组成的新数列的前 n 项的和,它也是等比数列求和公式推导的思想方法.类型一 等比数列前 n 项和的计算[例 1] (1)已知在等比数列{an}中,a1=2,S3=6,求 a3和 q.(2)在等比数列{an}中,Sn为其前 n 项和,公比为 q,若 Sn=189,q=2,an=96,求 a1和n.[分析] 运用等比数列的前 n 项和公式Sn=[解] (1)若 q=1,则 S3=3a1=6,符合题意.此时,a3=a1=2;若 q≠1,则由等比数列的前 n 项和公式,得 S3===6,解得 q=1(舍去)或 q=-2.此时,a3=a1q2=2×(-2)2=8.综上所述,q=1,a3=2 或 q=-2,a3=8.(2)方法一: Sn===(q≠1),∴189=,∴a1=3,又 an=a1qn-1,∴96=3×2n-1,即 2n-1=32,则 n=...