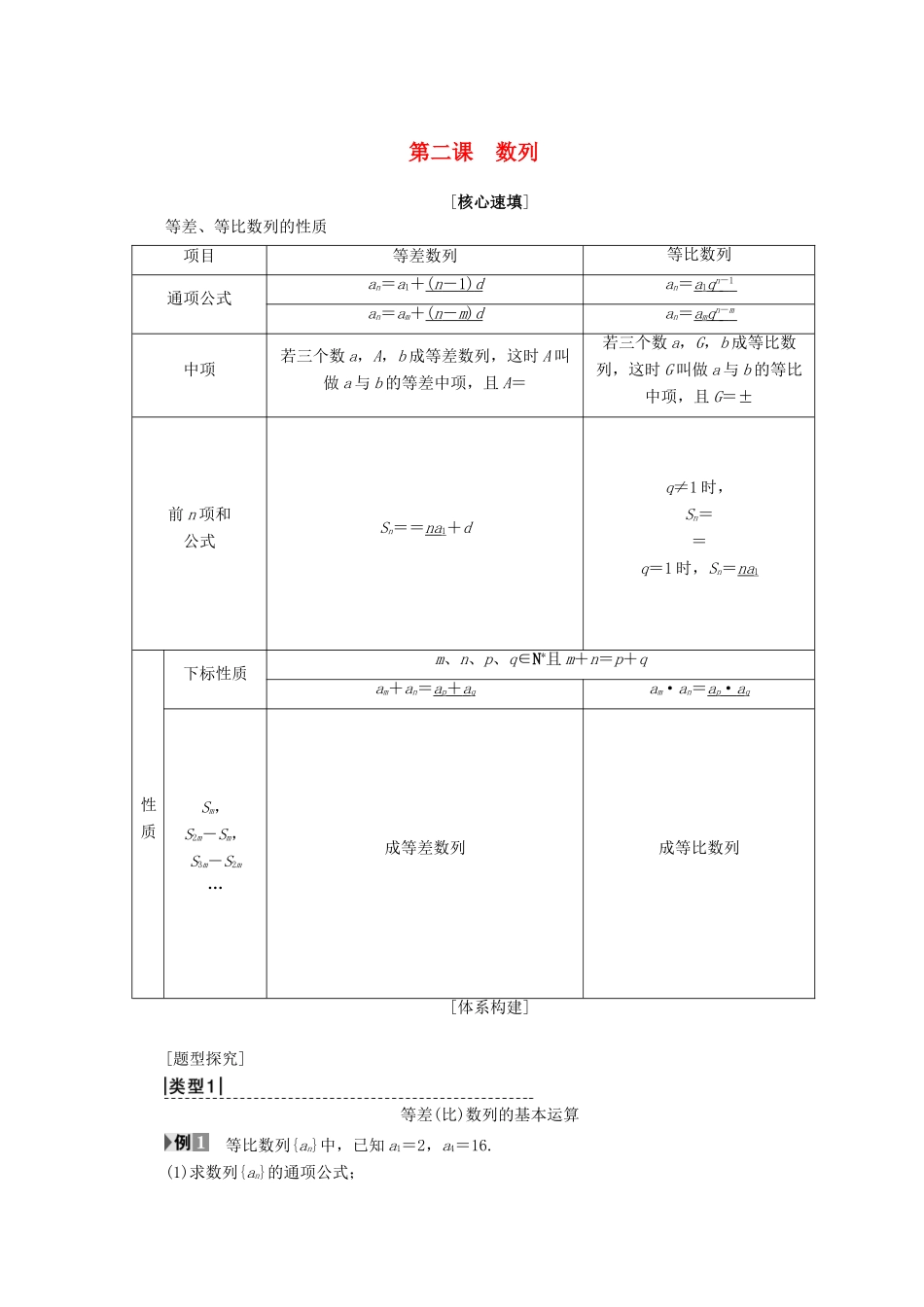
第二课 数列[核心速填]等差、等比数列的性质项目等差数列等比数列通项公式an=a1+( n - 1) d an=a1q n - 1 an=am+( n - m ) d an=amq n - m 中项若三个数 a,A,b 成等差数列,这时 A 叫做 a 与 b 的等差中项,且 A=若三个数 a,G,b 成等比数列,这时 G 叫做 a 与 b 的等比中项,且 G=±前 n 项和公式Sn==na1+dq≠1 时,Sn==q=1 时,Sn=na1性质下标性质m、n、p、q∈N*且 m+n=p+qam+an=ap+ a qam·an=ap· a qSm,S2m-Sm,S3m-S2m…成等差数列成等比数列[体系构建][题型探究]等差(比)数列的基本运算 等比数列{an}中,已知 a1=2,a4=16.(1)求数列{an}的通项公式;(2)若 a3,a5分别为等差数列{bn}的第 3 项和第 5 项,试求数列{bn}的通项公式及前 n 项和Sn.[解] (1)设{an}的公比为 q,由已知得 16=2q3,解得 q=2,∴an=2×2n-1=2n.(2)由(1)得 a3=8,a5=32,则 b3=8,b5=32.设{bn}的公差为 d,则有解得所以 bn=-16+12(n-1)=12n-28.所以数列{bn}的前 n 项和Sn==6n2-22n.[规律方法] 在等差数列和等比数列的通项公式 an与前 n 项和公式 Sn中,共涉及五个量:a1,an,n,d或q,Sn,其中 a1和 d或 q为基本量,“知三求二”是指将已知条件转换成关于 a1,dq,an,Sn,n的方程组,利用方程的思想求出需要的量,当然在求解中若能运用等差比数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.[跟踪训练]1.已知等差数列{an}的公差 d=1,前 n 项和为 Sn.(1)若 1,a1,a3成等比数列,求 a1;(2)若 S5>a1a9,求 a1的取值范围.【导学号:91432240】[解] (1)因为数列{an}的公差 d=1,且 1,a1,a3成等比数列,所以 a=1×(a1+2),即 a-a1-2=0,解得 a1=-1 或 a1=2.(2)因为数列{an}的公差 d=1,且 S5>a1a9,所以 5a1+10>a+8a1,即 a+3a1-10<0,解得-5