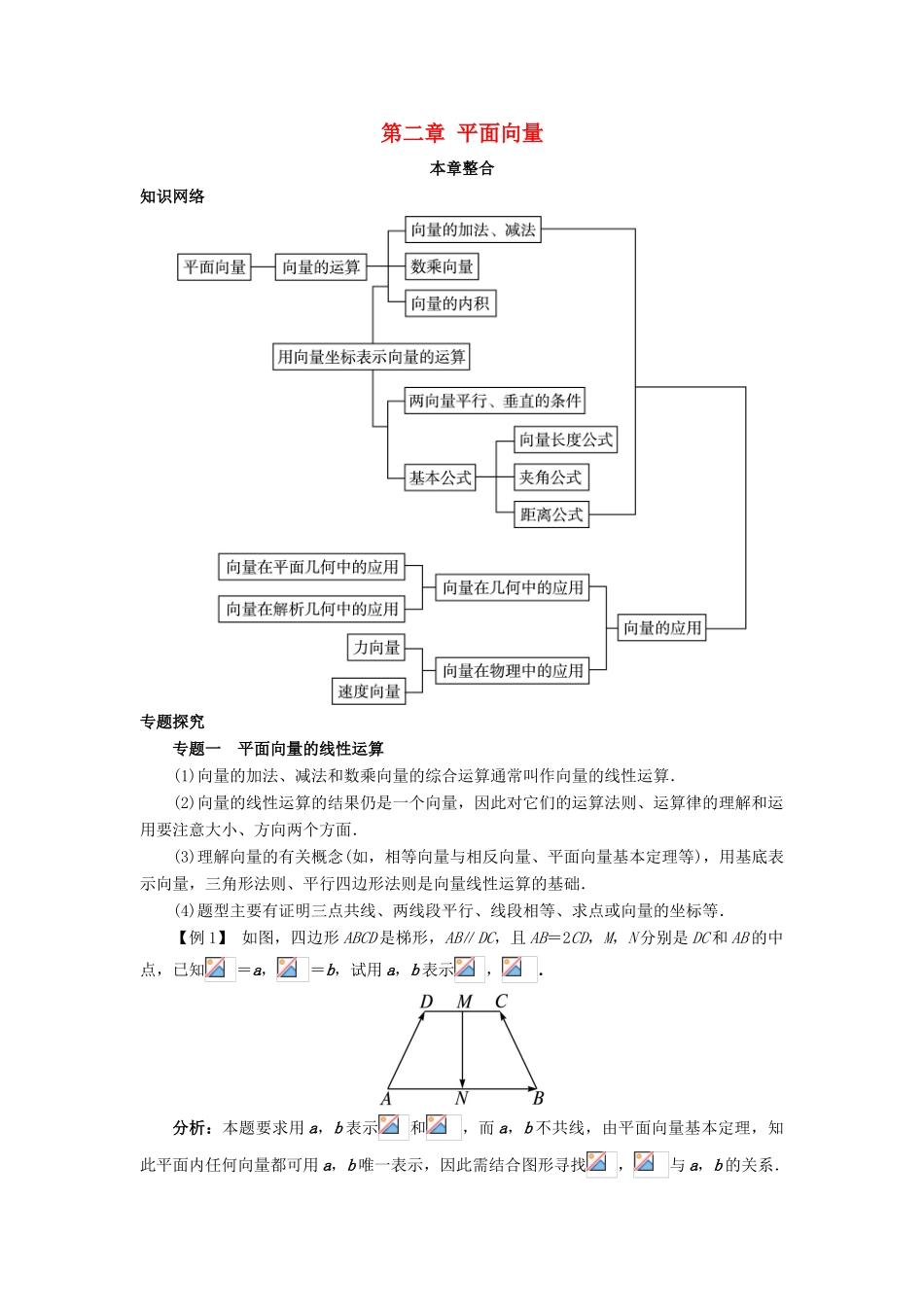
第二章 平面向量本章整合知识网络专题探究专题一 平面向量的线性运算(1)向量的加法、减法和数乘向量的综合运算通常叫作向量的线性运算.(2)向量的线性运算的结果仍是一个向量,因此对它们的运算法则、运算律的理解和运用要注意大小、方向两个方面.(3)理解向量的有关概念(如,相等向量与相反向量、平面向量基本定理等),用基底表示向量,三角形法则、平行四边形法则是向量线性运算的基础.(4)题型主要有证明三点共线、两线段平行、线段相等、求点或向量的坐标等.【例 1】 如图,四边形 ABCD 是梯形,AB∥DC,且 AB=2CD,M,N 分别是 DC 和 AB 的中点,已知=a,=b,试用 a,b 表示,.分析:本题要求用 a,b 表示和,而 a,b 不共线,由平面向量基本定理,知此平面内任何向量都可用 a,b 唯一表示,因此需结合图形寻找,与 a,b 的关系.解:如图,连接 DN,CN.因为 N 为 AB 的中点,且=a,所以==.又 AB=2CD,且 AB∥CD,所以§=§=§a.所以§=§=§a.所以在△ADN 中,§=§-§=§a-b,在△DMN 中,=-=-b-=-b,在△MNC 中,=-=-+b=b,在△NBC 中,=-=b-.所以=-+b,=-b.专题二 平面向量的坐标运算(1)向量的坐标运算把向量线性运算转化为代数运算,达到数与形的统一.(2)平面向量的坐标运算主要解决求向量的坐标,判断向量共线、平行等问题.【例 2】 已知 A(-1,0),B(0,2),C(-3,1),且·=5,2=10.(1)求 D 点的坐标;(2)用,表示.分析:利用待定系数法建立有关未知量的方程求解.解:(1)设 D 点的坐标为(x,y),则=(1,2),=(x+1,y),所以·=x+1+2y=5,①2=(x+1)2+y2=10.②联立①②,解得或所以 D 点的坐标为(-2,3)或(2,1).(2)当 D 点的坐标为(-2,3)时,=(1,2),=(-1,3),=(-2,1).设=m+n,则(-2,1)=m(1,2)+n(-1,3).所以所以所以=-+.当 D 点的坐标为(2,1)时,=(3,1).设=p+q,则(-2,1)=p(1,2)+q(3,1),所以所以所以=-.所以当 D 点的坐标为(-2,3)时,=-+;当 D 点的坐标为(2,1)时,=-.专题三 平面向量的数量积及其应用平面向量的数量积是向量的核心内容,向量的平行、垂直是向量中最基本、最重要的位置关系,而向量的夹角、长度是向量的数量特征,利用向量的数量积可以证明两个向量垂直、平行,求两个向量的夹角,计算向量的长度等.【例 3】 设 0<|a|≤2,f(x)=cos2x-|a|sin x-|b|的最大值为 0...