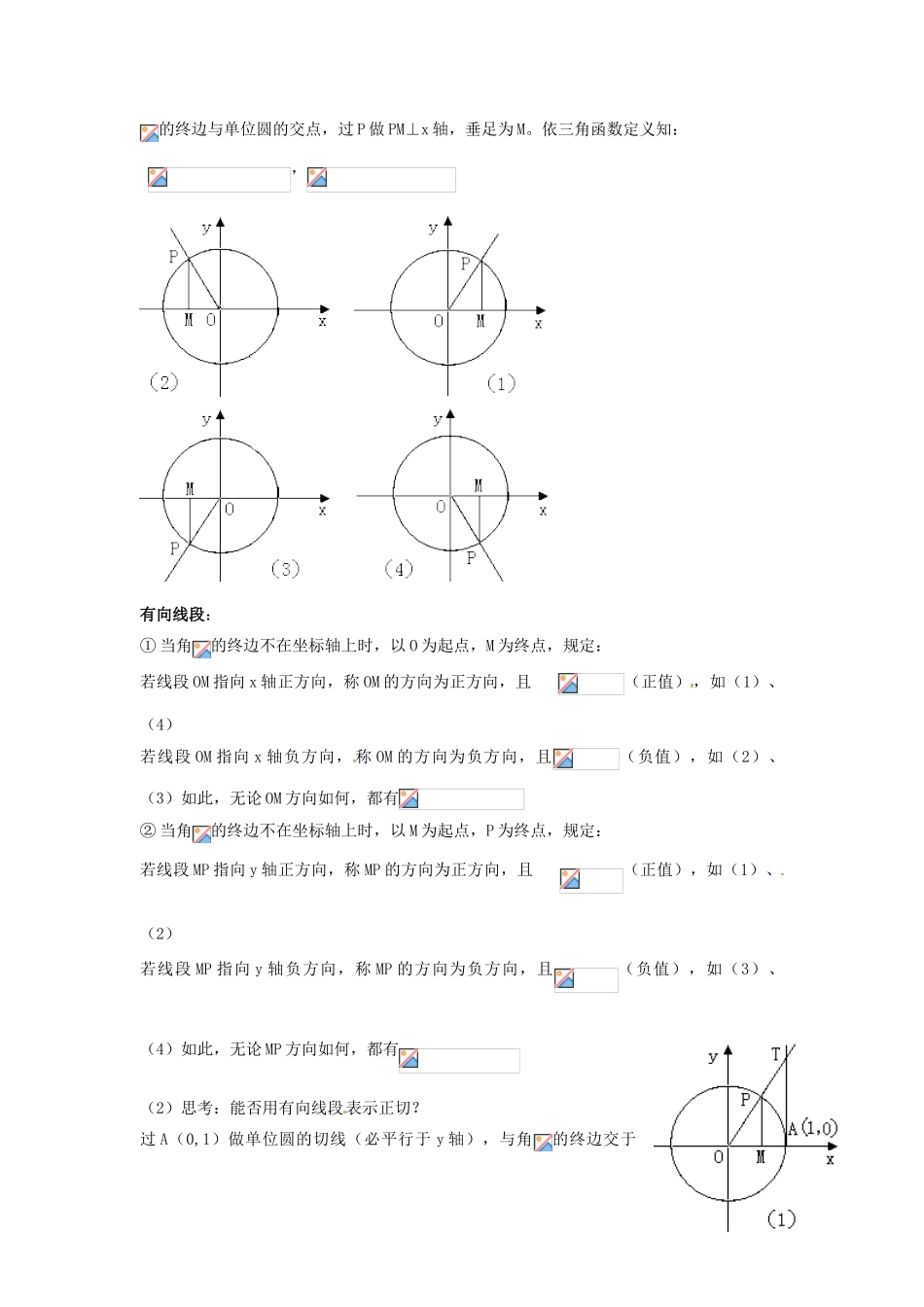
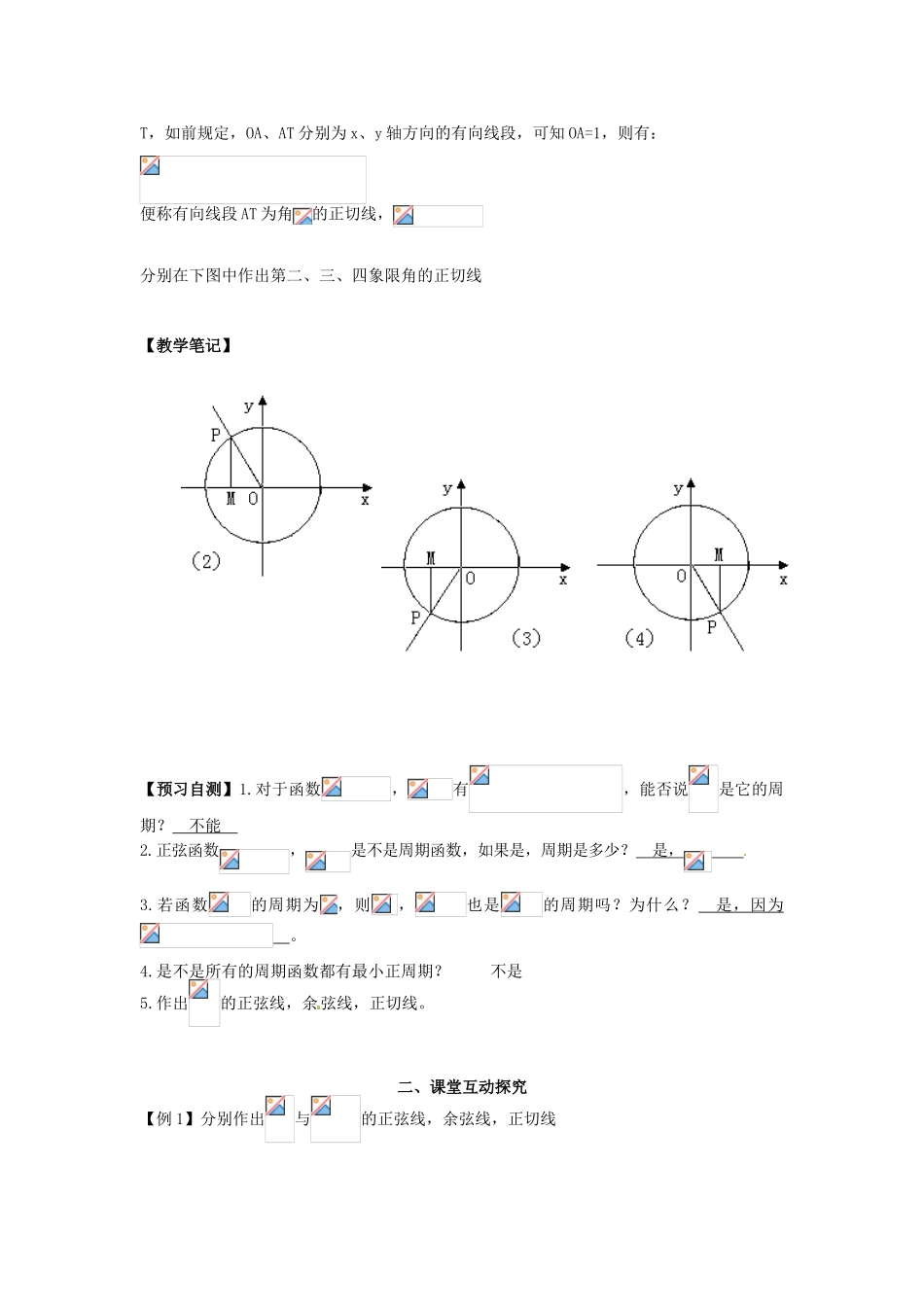
1.4.2 单位圆与周期性、三角函数线 导学案 一、课前自主导学【学习目标】1.通过正、余弦函数的周期现象,理解周期函数,周期函数的周期和最小正周期的定义;2.能根据周期函数的定义解决与周期性有关的问题;3.理解三角函数线的几何意义,能正确画出三角函数线;能利用三角函数线解决有关问题;【重点、难点】1.周期函数,周期函数的周期和最小正周期的定义;2.有关函数周期性的应用;3.三角函数线的几何意义及简单应用;【温故而知新】1.复习填空 (1)单位圆:以 单位长度 为半径的圆 (2)任意角的三角函数:设是一个任意角,角的终边与单位圆的交点, 那么角的正弦、余弦、正切分别是: (3)把某种动作或现象每经过一段时间后就会重复出现的现象叫做周期现象。(4)周期现象的特征:1、经过相同的时间间隔;2、现象是重复的。【教材助读】1.认真阅读课本 P15—16,理解正、余弦函数的周期现象,并掌握周期函数,周期函数的周期和最小正周期的定义,完成下列填空(1)终边相同的角的正、余弦值都相等,即有= ,= ;则正弦函数与余弦函数都为周期函数,且 是他们的最小正周期。(一般周期指的是最小正周期)(2)周期函数:一般地,对于函数,如果存在非零实数 T,对定义域的 任意一个值,都有 ,则称为周期函数,T 叫做周期函数的 周期 ;2.三角函数线的概念(1)如图(1)(2)(3)(4)分别表示终边在一、二、三、四象限的角,为的终边与单位圆的交点,过 P 做 PM⊥x 轴,垂足为 M。依三角函数定义知: ,有向线段:① 当角的终边不在坐标轴上时,以 O 为起点,M 为终点,规定:若线段 OM 指向 x 轴正方向,称 OM 的方向为正方向,且 (正值) ,如(1)、(4)若线段 OM 指向 x 轴负方向, 称 OM 的方向为负方向,且(负值),如(2)、(3)如此,无论 OM 方向如何,都有② 当角的终边不在坐标轴上时,以 M 为起点,P 为终点,规定:若线段 MP 指向 y 轴正方向,称 MP 的方向为正方向,且 (正值),如(1)、(2)若线段 MP 指向 y 轴负方向,称 MP 的方向为负方向,且(负值),如(3)、(4)如此,无论 MP 方向如何,都有(2)思考:能否用有向线段表示正切?过 A(0,1)做单位圆的切线(必平行于 y 轴),与角的终边交于T,如前规定,OA、AT 分别为 x、y 轴方向的有向线段,可知 OA=1,则有:便称有向线段 AT 为角的正切线,分别在下图中作出第二、三、四象限...