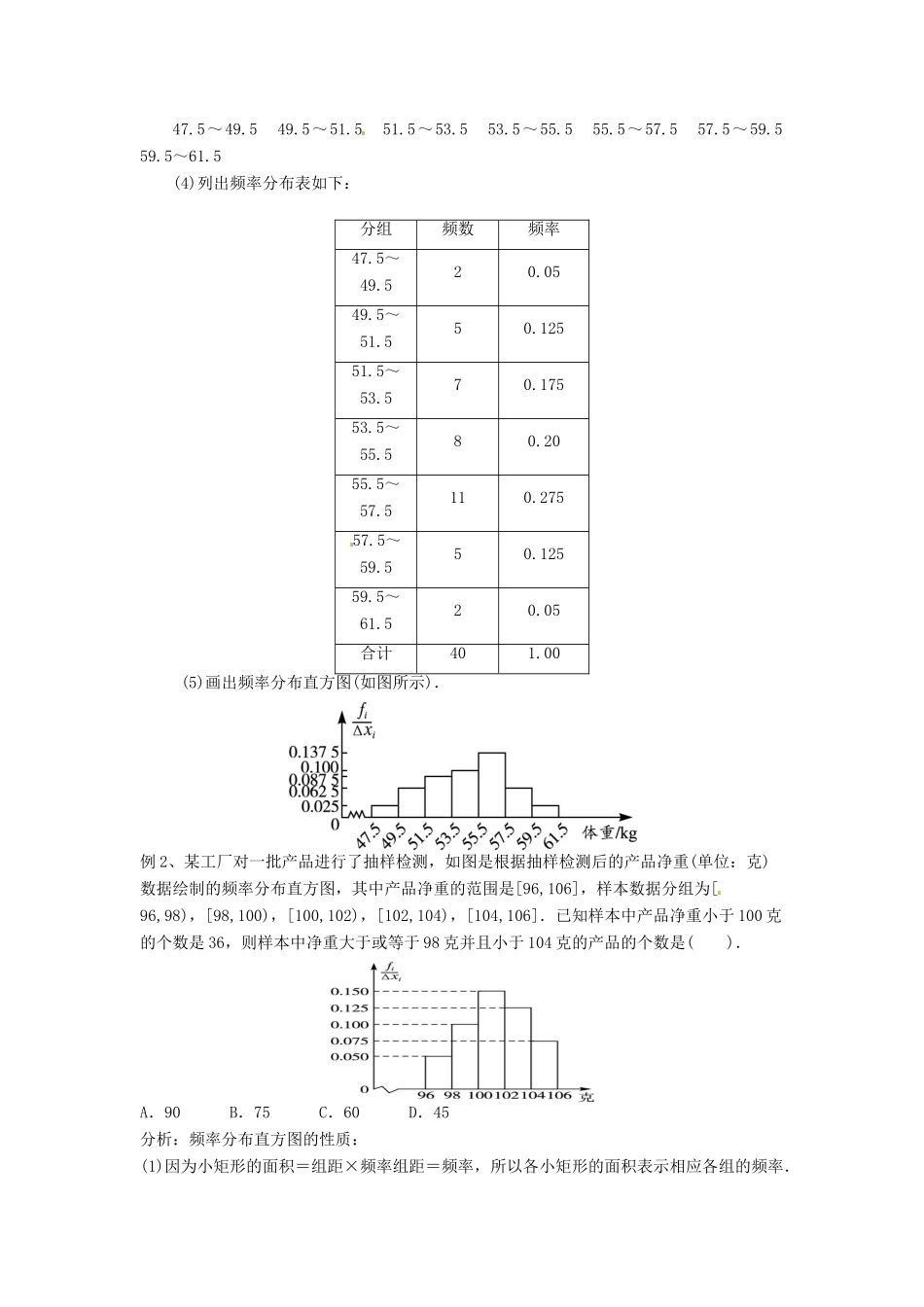
1.5 用样本估计总体 一、课前自主导学【教学目标】 1.通过实例体会分布的意义与作用,学会列频率分布表,画频率分布直方图及频率折线图.2.能根据具体问题选择恰当的图表分析样本的分布.3.体会用样本估计总体的思想,认识到数学知识源于生活并指导生活的事实.【重点难点】重点:列频率分布表,画频率分布直方图、频率折线图.难点:通过样本的频率分布及数字特征估计总体的分布及数字特征.【教材助读】课前认真通读课本 P32-P37;频率分布表和频率分直方布图,是从各个小组数据在样本容量中所占比例大小的角度,来表示数据分布的规律.频率分布是指一个样本数据在各个小范围内所占比例的大小;一般用频率分布直方图反映样本的频率分布.1. 绘制频率分布直方图的步骤为: (1)求极差,即计算 一组数据中最大值与最小值的差,也称为全距 ;(2)决定组距与组数, 组距=;(3)将数据分组(分组区间一般左闭右开);(4)统计频数并计算频率,列出 频率分布 ;(5)画频率分布直方图.(其中前 4 步为列频率分布表的步骤)2.在频率分布直方图中,每一个小长方形的面积=组距×= 频率 ,且各小长方形的面积的总和等于 1 .3.关于频率分布直方图的几点说明:(1)从频率分布直方图可以清楚地看出数据分布的总体趋势.(2)把数据表示成频率分布直方图后,原始数据信息就被抹掉了.(3)同一组数据,若组距不同,横、纵轴的单位不同,得到的图和形状也会不同.(4)频率分布直方图是用面积表示各组频率的多少,矩形的高度表示每一组的频率组距,宽度则表示各组的组距;而条形图是用条形的高度表示各类别频数大小.4.频率折线图在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各矩形的 上底边中点 ,直至右边所加区间的 中间 ,就可以得到一条折线,称之为 频率折线图 .作频率折线图时随着所分的组数的增加,组距减小,相应的 折线 图会越来越接近于一条光滑曲线. 5.估计总体的数字特征若利用简单随机抽样方法得到的样本数据分别为…,则样本平均值=;样本标准差=.【预习自测】1.关于频率分布直方图中的有关数据,下列说法正确的是 ( D )A.矩形的高表示该组上的个体在样本中出现的频率B.矩形的高表示取某数的频率C.矩形的高表示该组上的个体数D.矩形的高表示该组上的个体在样本中出现的频率与组距的比值2.一个容量为 20 的样本数据, 数据的分组及各组的频数如下:[1...