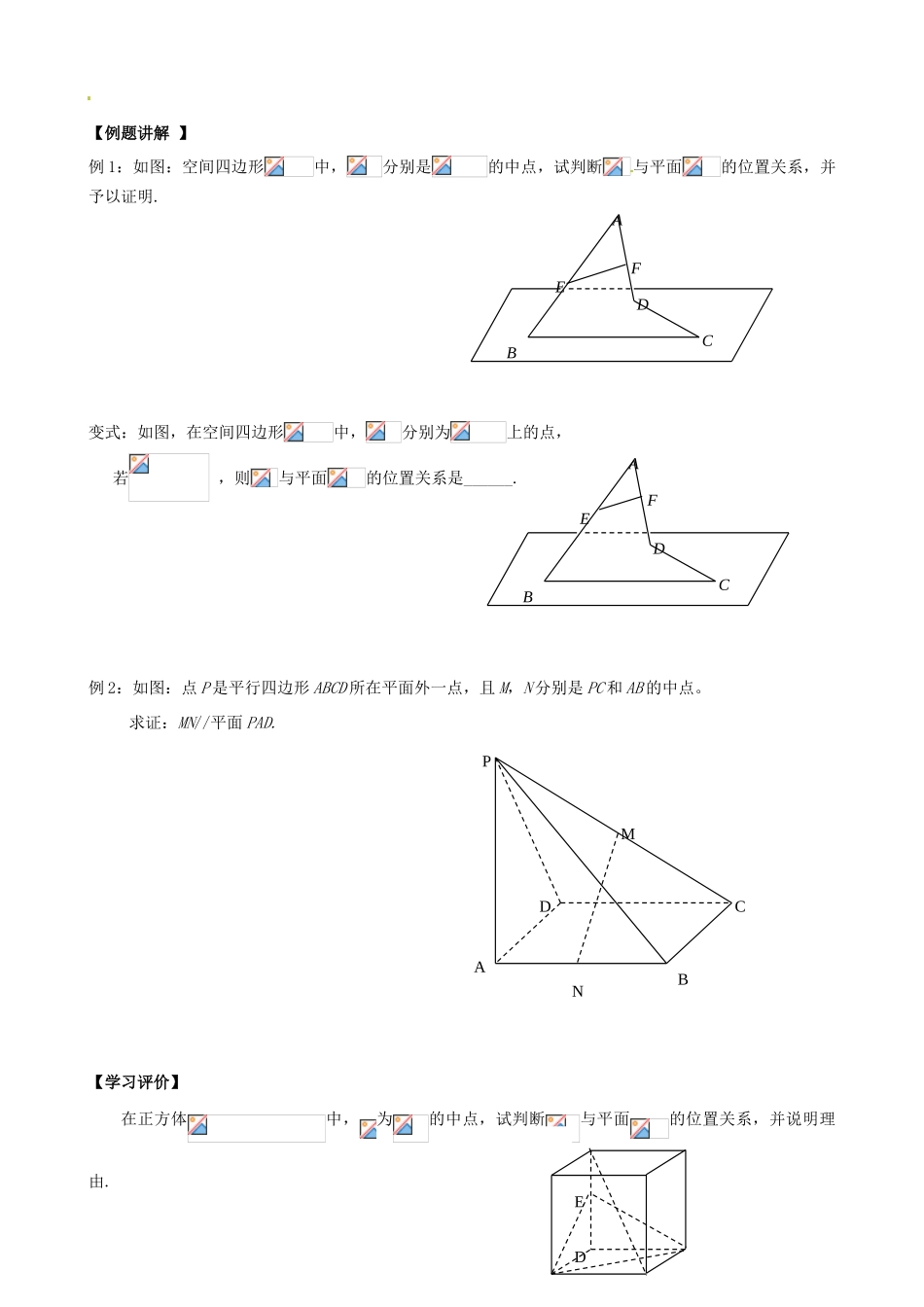
直线与平面平行的判定 学习目标 1、知识与技能:(1)理解并掌握直线与平面平行的判定定理; (2)能应用定理证明简单的线面平行问题。2、过程与方法:学生由生活中的例子,通过观察、操作、探究、猜想等合情推理活动,归纳出线面平行的判定定理.3、情感、态度与价值观:(1)让学生在发现中学习,增强学习的积极性; (2)让学生了解空间与平面互相转化的数学思想。学习重、难点重点:直线与平面平行的判定定理的探索过程及应用.难点:直线与平面平行的判定定理的理解及应用.学法与教具1、学法:学生借助实例,通过观察、思考、交流、讨论等,理解判定定理。2、教学用具:多媒体 学习过程 一、课前准备(预习教材 P54至 P55,找出疑惑之处)复习:1、观察图片,说说直线和平面都有哪些位置关系?并用图形及符号表示直线与平面的位置关系。2、如何定义直线与平面平行的?你如何保证它们没有公共点呢?3、根据日常生活的观察,你能感知并举出直线与平面平行的具体事例吗?讨论:直线和平面的位置关 系中,平行是最重要的关系之一,那么如何判定直线和平面是平行的呢?根据定义好判断吗?二、新课导学※ 探索新知探究1:准备直角梯形(操作感知,猜想定理)当把直角腰放在桌面上并转动,观察另一腰所在直线与桌面所在的平面具有什么样的位置关系?当把梯形的一条底边放在桌面上并转动,观察另一底边所在直线与桌面所在的平面具有D什么样的位置关系?直线在桌面所在的平面 (填“内”或“外”)直线在桌面所在的平面 (填“内”或“外”)直线与始终是 问题:上面实例中的直线为什么会和对应的平面平行呢?你能猜想出什么结论吗?能作图把这一结论表示出来吗?探究 2:直线与平面平行的判定定理(合作探究,确认定理)平面外 与此平面内的一条直线 ,则该直线与此平面平行. 请你思考下列问题:⑴ 怎样用图形语言和符号语言表示上述定理;图形语言: 符号语言:⑵ 上述定理的实质是什么?它体现了什么数学思想?对于空间几何的问题我们该怎么处理?【基础练习】(质疑反思,深化定理) 1、 判断下列命题是否正确,若不正确,请用图形语言或模型加以表达。(1)若直线在平面外,则( )(2)若直线平行于平面内的无数条直线,则( ).(3)( )(4)( )(5)( )2、如图,长方体中,(1)与平行的平面是________________(2)与平行的平面是________________(3)与平行的平面是________________【例题讲解 】例 1:...