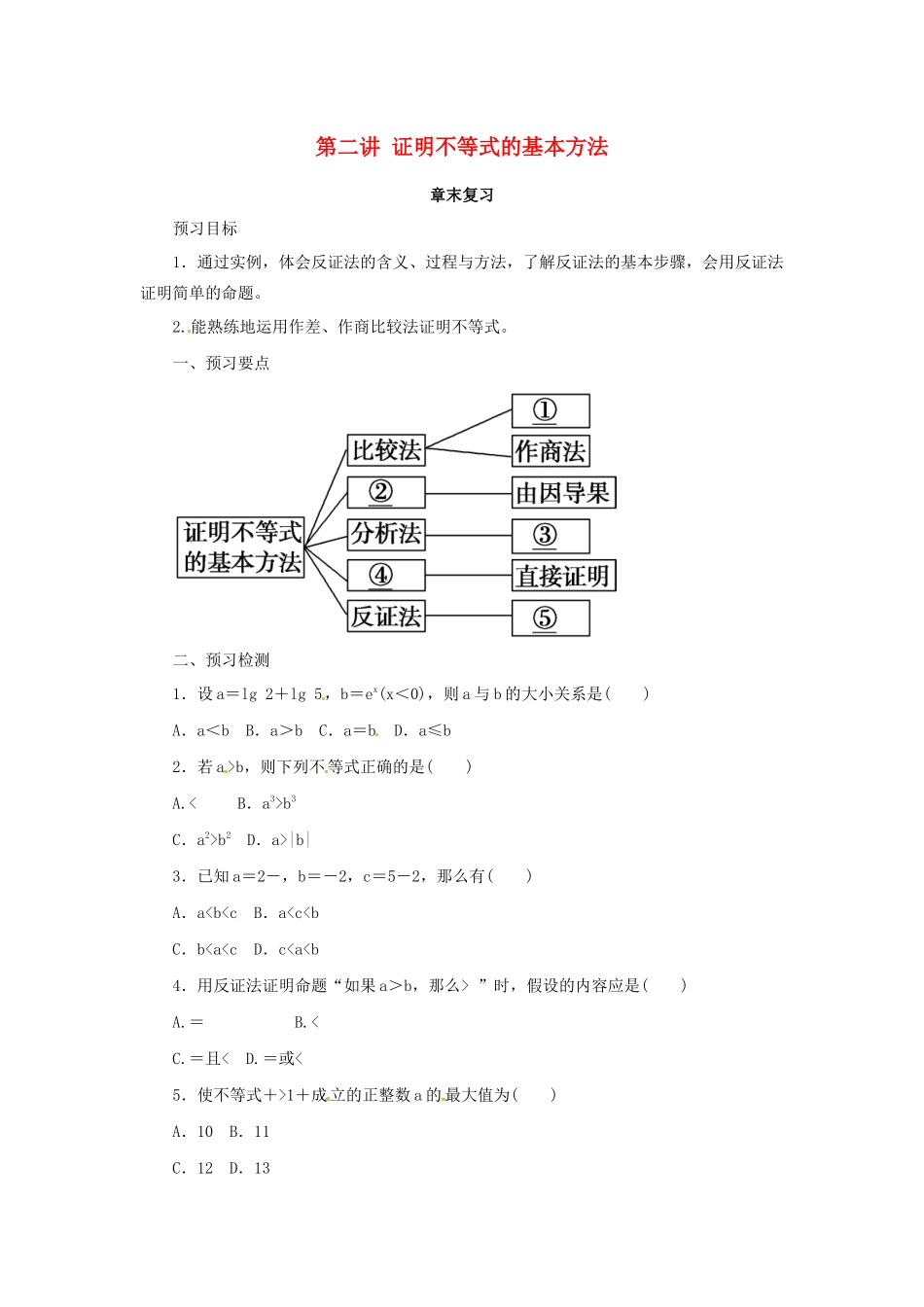
第二讲 证明不等式的基本方法章末复习预习目标1.通过实例,体会反证法的含义、过程与方法,了解反证法的基本步骤,会用反证法证明简单的命题。2.能熟练地运用作差、作商比较法证明不等式。一、预习要点 二、预习检测1.设 a=lg 2+lg 5,b=ex(x<0),则 a 与 b 的大小关系是( ) A.a<b B.a>b C.a=b D.a≤b2.若 a >b,则下列不等式正确的是( )A.< B.a3>b3C.a2>b2 D.a>|b|3.已知 a=2-,b=-2,c=5-2,那么有( )A.a
”时,假设的内容应是( )A.= B.1+成立的正整数 a 的 最大值为( )A.10 B.11C.12 D.13三、思学质疑把你在本次课程学习中的困惑与建议填写在下面,与同学交流后,由组长整理后并拍照上传平台讨论区。参考答案一、预习要点① 作差法② 综合法③ 执果索因④ 放缩法⑤ 间 接证明二、预习检测1.解析:选 B ∵a=lg 2+lg 5=1,b=ex(x<0),故 b<1,∴ a>b.2.解析:选 B 若 a=1,b=-3,则>,a2b,则 a3>b3.3.解析:选 A ∵a-b=(2-)-(-2)=4-2<0,∴a<b.b-c=(-2)-(5-2)=(-2)(1-)<0,∴b,=,<三方面的关系,所以>的反设应为=或<.5.解析:选 C 用分析法可证 a=12 时不等式成立,a=13 时不等式不成立.