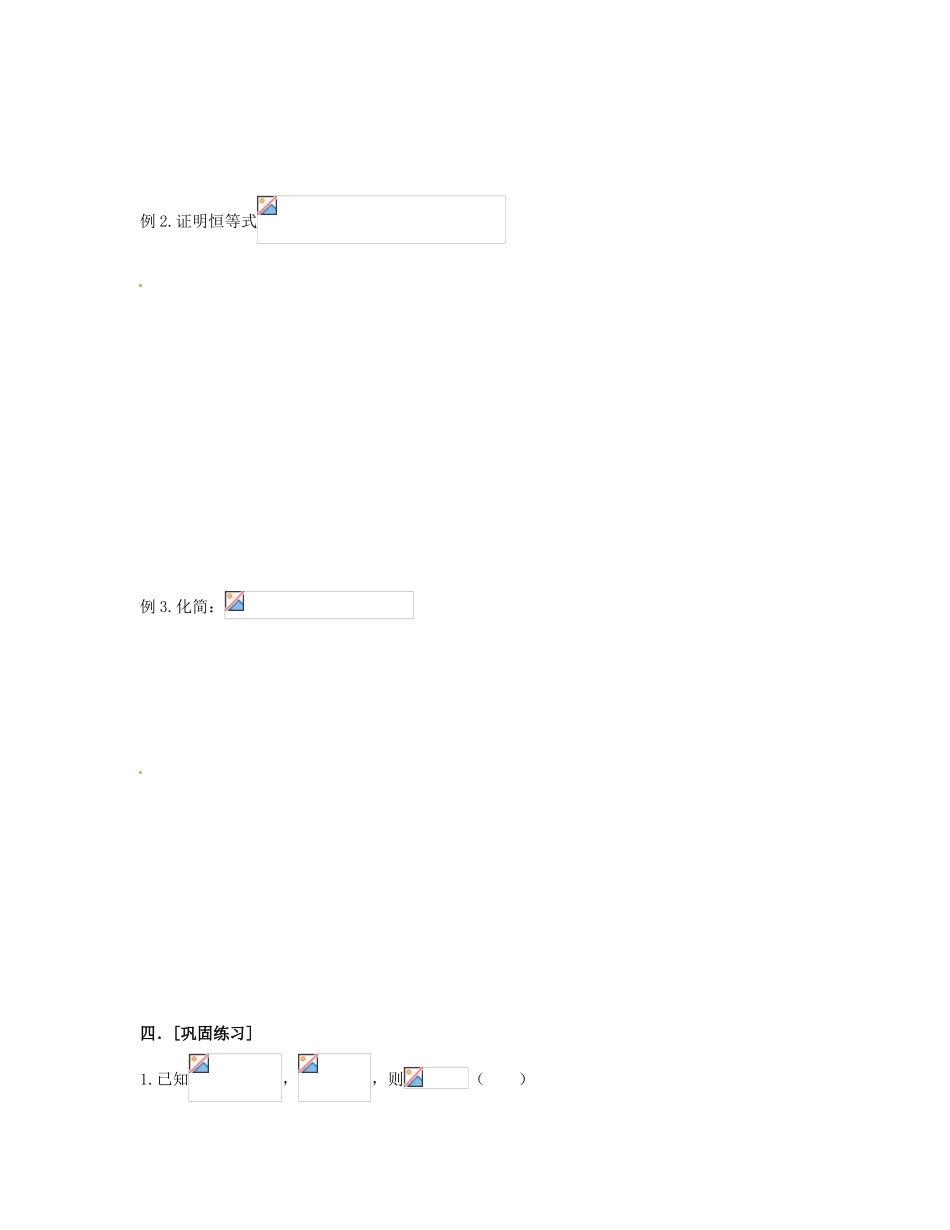
3.2.1 倍角公式编者: 校审: 组长:一、[学习关键词]1.能够运用正弦、余弦、正切和角公式,推导出它们对应的倍角公式及公式的两种变形.2.能够运用公式进行简单三角函数式的化简、求值与恒等式的证明.3.能够推导倍角公式,了解它们之间,以及它们与和角公式之间的内联系.二、[课前自主梳理] 1.倍角公式(1) ,其中角是 角,它是和角公式中 时的特例。(2) ,利用,还可变形为 和 (3) ,其中必须满足 2.倍角公式的变形(1) = (2)= (3) (4) (5) 三、[课堂合作研习]例 1 已知,,求的值.例 2.证明恒等式例 3.化简:四.[巩固练习]1.已知,,则( )A.B.C.D.2.=( )A.B.C.D.3.是( )A.最小正周期为的偶函数B.最小正周期为的奇函数C.最小正周期为的偶函数D.最小正周期为的奇函数4. 5.若,且,则 6.已知,,求的值.3.2.1 倍角公式【强化练习】1.则的值为( )A. B. C. D.2.若,则( )A.B.C.D.3.函数的最小值和最大值分别为( )A.-3,1B.-2,2C.-3,D.4.已知函数,则是( )A.最小正周期为的奇函数 B.最小正周期为的奇函数 C.最小正周期为的偶函数 D.最小正周期为的偶函数 5.若,则的值为( )A. B. C.D. 6.化简(1) (2)= 7.已知.(1)求的值;(2)求的值.8.已知函数,求函数的最大值及对应自变量的集合.9.已知函数 的最小正周期为.(1)求的值;(2)求函数在区间上的取值范围.3.2.1 倍角公式【强化练习】答案1.C 解:∴∴∴2.B 解:由∴=∴ 由 ∴∴3.C 解:令,则,所以其对称轴∴时时∴4.D 解:∴,又对任意∴函数为偶函数6.(1) 解:原式=(2)解:原式=7.(1)解:∵,∴原式(2)由(1)知8.解:∴当即时故,的集合为9.解:(1)∵∴ ∴(2)由(1)知∵∴∴∴∴在上的取值范围为