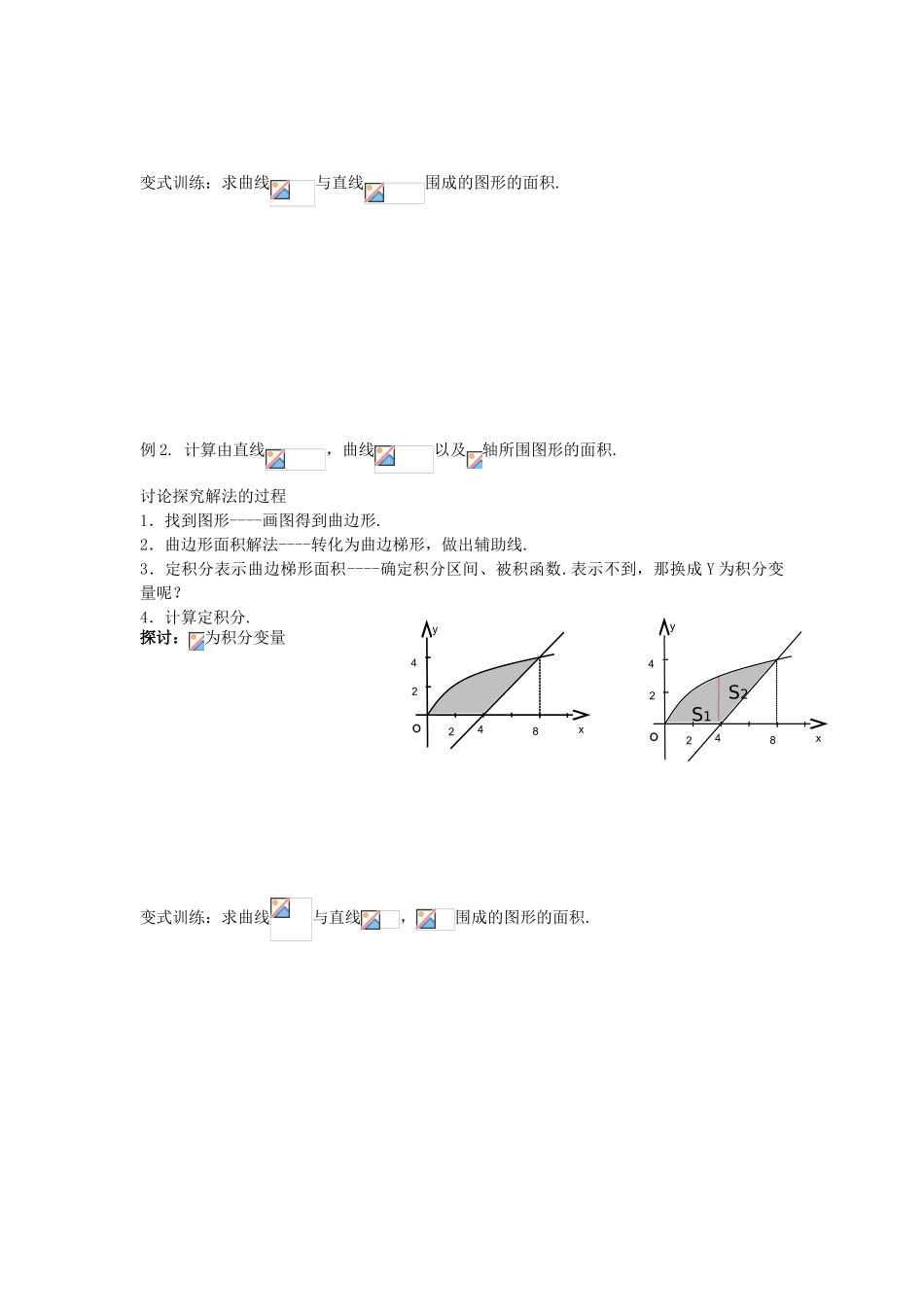
定积分的简单应用一 学习目标:1.使学生在定积分几何意义的基础上,通过自主探究,应用定积分解决曲线围成的平面图形的面积.2.能应用定积分求变速直线运动的路程、变力所做的功.二 重点难点:重点:能够利用定积分解决实际问题,在解决问题的过程中体会定积分的价值.难点:如何恰当选择积分变量和确定被积函数三 知识链接定积分的概念、定积分的计算、定积分的几何意义四 学习指导图形的面积为非负数,当图形在轴的下方时的情况需要注意;当图形比较复杂时,将图形分割成若干个比较简单的图形; 在物理中应用时,注意力或速度的方向,积分的上限、下限.五 问题逻辑(一)复习与思考1.定积分的几何意义 .热身训练:计算(1) (2).计算 2.用定积分表示阴影部分的面积3.汽车变速直线运动行驶的路程 ,等于其速度函数在时间区间[,]上的定积分,即 .4.如果物体在变力的作用下做直线运动,并且物体沿着与相同的方向从移动到(),那么变力所做的功为 .(二)定积分在几何中的应用例1.计算由曲线与所围图形的面积.探究过程.1.找到图形----画图得到曲边形.2.曲边形面积解法----转化为曲边梯形,做出辅助线.3.定积分表示曲边梯形面积----确定积分区间、被积函数.4.计算定积分.xyNMOABCDxyNMObABCDxyOABCD11-1-1变式训练:求曲线与直线围成的图形的面积.例 2. 计算由直线,曲线以及轴所围图形的面积.讨论探究解法的过程1.找到图形----画图得到曲边形.2.曲边形面积解法----转化为曲边梯形,做出辅助线.3.定积分表示曲边梯形面积----确定积分区间、被积函数.表示不到,那换成 Y 为积分变量呢?4.计算定积分.探讨:为积分变量变式训练:求曲线与直线,围成的图形的面积.4xyO8422x4yO8422S1S2反思:解由曲线所围的平面图形面积的解题步骤:1.画草图,求出曲线的交点坐标.2.将曲边形面积转化为曲边梯形面积.3.根据图形特点选择适当的积分变量.(注意选择型积分变量时,要把函数变形成用表示的函数)4.确定被积函数和积分区间.5.计算定积分,求出面积.(三)定积分在物理中的应用(变速直线运动的路程)例 3.(见课本例 3)变式训练:一点在直线上从时刻开始以速度运动,求(1)在时的位置;(2)在时运动的路程.(四)定积分在物理中的应用(变力做功)例 4.(见课本例 4)变式训练:在底面积为的圆柱容器中盛有一定量的气体,在等温条件下,由于气体的膨胀,把容器中的一个活塞(面积为)从处推到处,计算在移动过程中,...