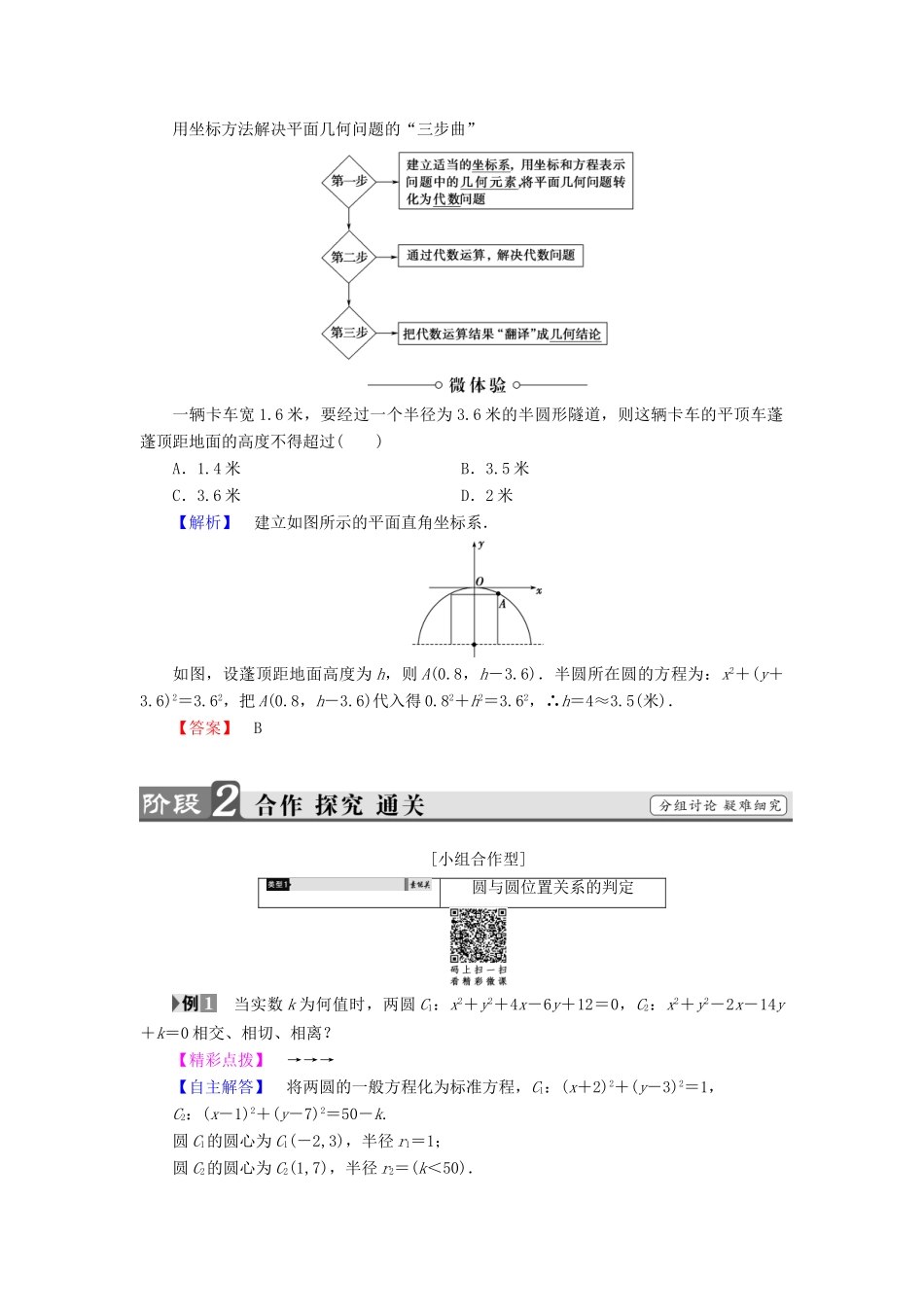
4.2.2 圆与圆的位置关系4.2.3 直线与圆的方程的应用1.掌握圆与圆的位置关系及判定方法.(重点、易错点)2.能利用直线与圆的位置关系解决简单的实际问题.(难点)[基础·初探]教材整理 1 圆与圆位置关系的判定阅读教材 P129至 P130“练习”以上部分,完成下列问题.1.几何法:若两圆的半径分别为 r1、r2,两圆的圆心距为 d,则两圆的位置关系的判断方法如下:位置关系外离外切相交内切内含图示d 与 r1、r2的关系d > r 1+ r 2d = r 1+ r 2| r 1- r 2|< d < r 1+ r 2d = | r 1-r2|0≤ d < | r 1- r 2|2.代数法:通过两圆方程组成方程组的公共解的个数进行判断.――→一元二次方程两圆 x2+y2=9 和 x2+y2-8x+6y+9=0 的位置关系是( )A.外离B.相交C.内切D.外切【解析】 两圆 x2+y2=9 和 x2+y2-8x+6y+9=0 的圆心分别为(0,0)和(4,-3),半径分别为 3 和 4.所以两圆的圆心距 d==5.又 4-3<5<3+4,故两圆相交.【答案】 B教材整理 2 直线与圆的方程的应用阅读教材 P130“练习”以下至 P132“练习”以上部分,完成下列问题.用坐标方法解决平面几何问题的“三步曲”一辆卡车宽 1.6 米,要经过一个半径为 3.6 米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过( )A.1.4 米B.3.5 米C.3.6 米D.2 米【解析】 建立如图所示的平面直角坐标系.如图,设蓬顶距地面高度为 h,则 A(0.8,h-3.6).半圆所在圆的方程为:x2+(y+3.6)2=3.62,把 A(0.8,h-3.6)代入得 0.82+h2=3.62,∴h=4≈3.5(米).【答案】 B[小组合作型]圆与圆位置关系的判定 当实数 k 为何值时,两圆 C1:x2+y2+4x-6y+12=0,C2:x2+y2-2x-14y+k=0 相交、相切、相离?【精彩点拨】 →→→【自主解答】 将两圆的一般方程化为标准方程,C1:(x+2)2+(y-3)2=1,C2:(x-1)2+(y-7)2=50-k.圆 C1的圆心为 C1(-2,3),半径 r1=1;圆 C2的圆心为 C2(1,7),半径 r2=(k<50).从而|C1C2|==5.当 1+=5,k=34 时,两圆外切.当|-1|=5,=6,k=14 时,两圆内切.当|r2-r1|<|C1C2|<r2+r1,即 14<k<34 时,两圆相交.当 1+<5 或|-1|>5,即 0≤k<14 或 34<k<50 时,两圆相离.1.判断两圆的位置关系或利用两圆的位置关系求参数的取值范围有以下几个步骤:(1)化成圆的标准方程,写出圆心和半径;(2)计算两圆圆...