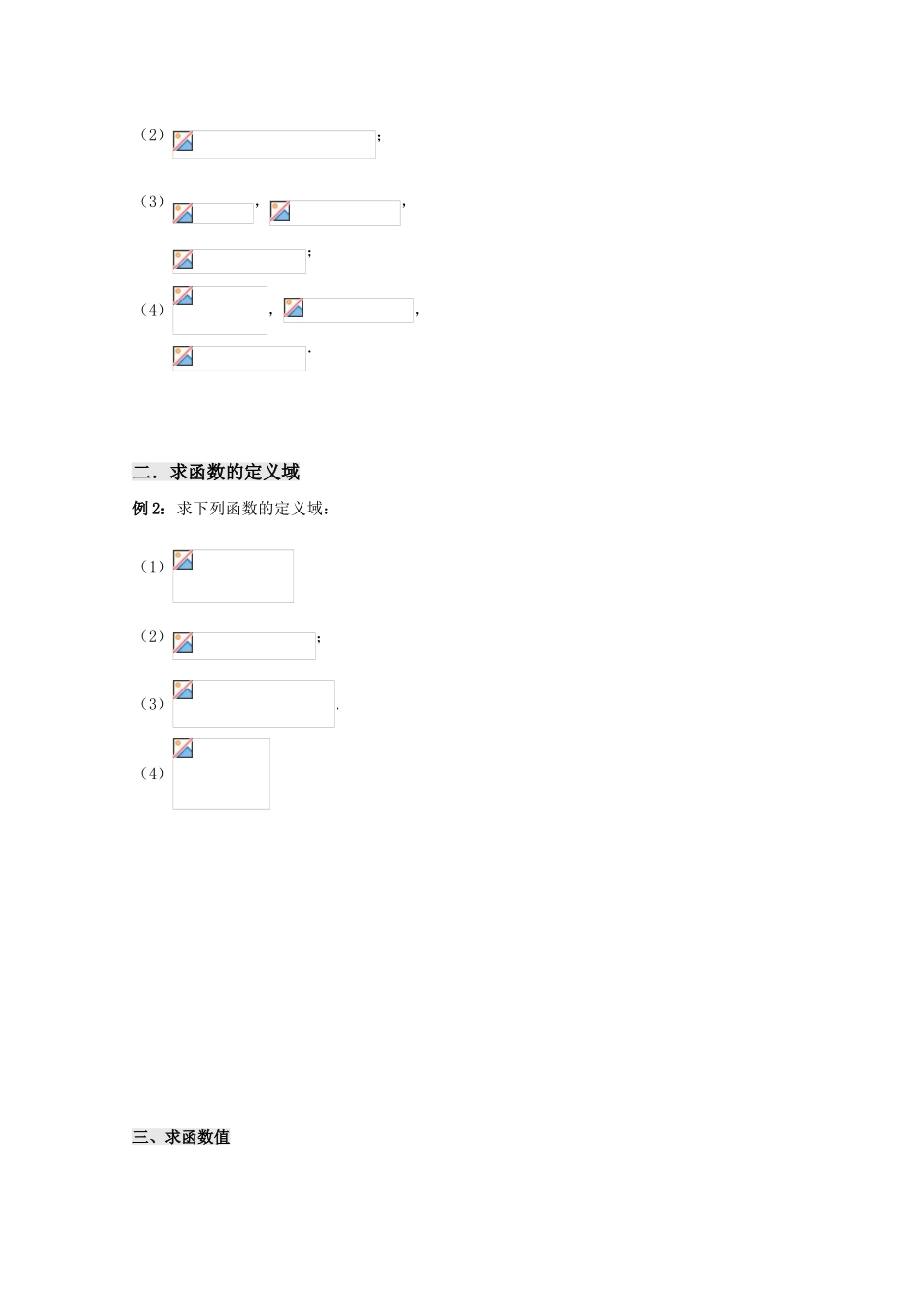
第一课时 函数的概念和图象导学案【学习导航】 知识网络 学习目标 1.理解函数概念;2.了解构成函数的三个要素; 3.会求一些简单函数的定义域与值域;4.培养理解抽象概念的能力.新课导学1. 函数的定义:设是两个 数集,如果按某种对应法则,对于集合中的 元素,在集合中都有 的元素和它对应,这样的对应叫做从到的一个函数,记为 .其中 组成的集合叫做函数的定义域, 的取值集合叫做函数的值域。【互动探究】一.对函数的定义的理解例 1:判断下列对应是否为函数:(1)函数函数定义函数的定义域函数的值域(2);(3),,;(4),,.二.求函数的定义域例 2:求下列函数的定义域:(1)(2); (3).(4)三、求函数值 例 3: 已知函数的定义域为,求的值.分析:求的值,即当时,求的值例 4:比较下列两个函数的定义域与值域:(1)f(x)=(x+2)2+1,x∈{-1,0,1,2,3};(2).【迁移应用】1. 对于集合,,有下列从到的三个对应:① ;②;③;其中是从到的函数的对应的序号为 ;2. 函数的定义域为 ____________3. 函数 f(x)=x-1(且)的值域为 .4.若,则 ;5.函数的定义域为 ;6.已知函数的定义域为[-2,3],则函数的定义域为 . 函数的概念和图象(1)2. 函数的定义:设是两个非空数集,如果按某种对应法则,对于集合中的每一个元素,在集合中都有惟一的元素和它对应,这样的对应叫做从到的一个函数,记为.其中输入值组成的集合叫做函数的定义域,所有输出值的取值集合叫做函数的值域。【精典范例】例 1:判断下列对应是否为函数:(1)(2);(3),,;(4),,.【分析】解本题的关键是抓住函数的定义,在定义的基础上输入一些数字进行验证,当不是函数时,只要列举出一个集合中的即可.【解】(1)是;(2)不是;(3)不是;(4)是。点评:判断一个对应是否是函数,要注意三个关键词:“非空”、“每一个”、“惟一”。例 2:求下列函数的定义域:(1)(2); (3).【解】(1);(2);(3)。点评: 求函数的定义域时通常有以下几种情况:① 如果是整式,那么函数的定义域是实数集;② 如果是分式,那么函数的定义域是使分母不等于零的实数的集合;③ 如果为二次根式,那么函数的定义域是使根号内的式子大于或等于 0 的实数的集合;④ 如果是由几部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数的集合。例 3:比较下列两个函数的定义域与值域:(...