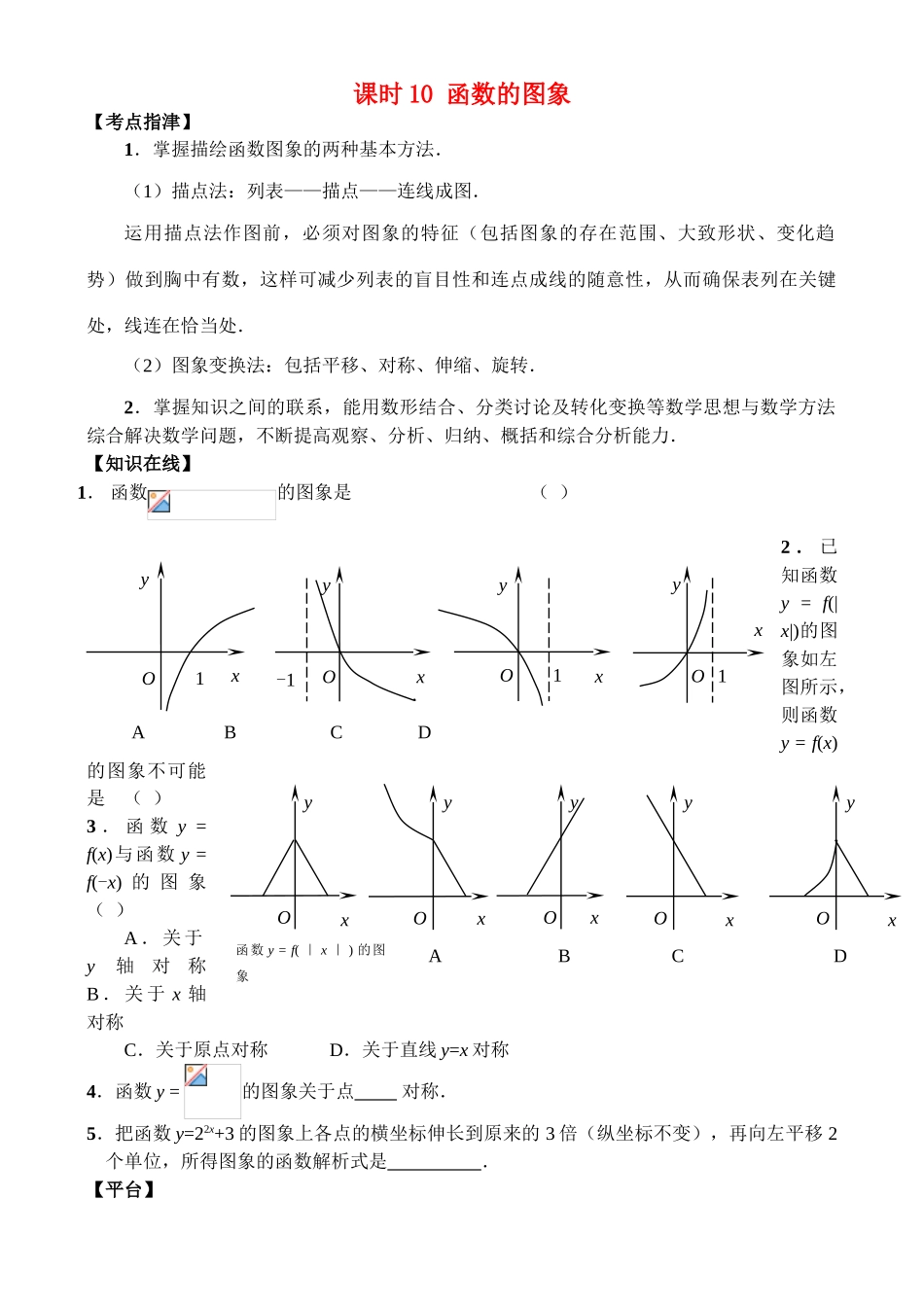
课时 10 函数的图象【考点指津】1.掌握描绘函数图象的两种基本方法.(1)描点法:列表——描点——连线成图.运用描点法作图前,必须对图象的特征(包括图象的存在范围、大致形状、变化趋势)做到胸中有数,这样可减少列表的盲目性和连点成线的随意性,从而确保表列在关键处,线连在恰当处.(2)图象变换法:包括平移、对称、伸缩、旋转.2.掌握知识之间的联系,能用数形结合、分类讨论及转化变换等数学思想与数学方法综合解决数学问题,不断提高观察、分析、归纳、概括和综合分析能力.【知识在线】1. 函数的图象是 ( )2 . 已知函数y = f(|x|)的图象如左图所示,则函数y = f(x)的图象不可能是 ( )3 . 函 数 y = f(x)与函数 y = f(-x) 的 图 象 ( )A . 关 于y轴对称 B . 关 于 x 轴对称C.关于原点对称 D.关于直线 y=x 对称4.函数 y = 的图象关于点 对称.5.把函数 y=22x+3 的图象上各点的横坐标伸长到原来的 3 倍(纵坐标不变),再向左平移 2个单位,所得图象的函数解析式是 .【平台】Oxy函数 y = f( | x | ) 的图象OxyOxyOxyOxyABCDxy1Oxy-1Oxxy1Oy1OA B C D例 1 作出下列各函数的图象: (1)y=10|lgx|;(2)y=x -|x-1|;(3)y= |x2-4x+3|.分析 以上图象用列表描点法作图有困难,为此应先对函数式进行变形,再利用熟悉的函数图形作图.解 (1)因|lgx| = ,于 是 , 当 x≥1 时 , 10|lgx| =10lgx = x;当 0<x<1 时,10|lgx| = 10-lgx = .故y=10|lgx| = .根据直线与反比例函数直接作出该分段函数的图象,如图 1 所示.(2)根据绝对值的意义,可将函数式化为分段函数 y=,可见其图象是由两条射线组成,图象如图 2.(3)解法一 去绝对值,得 y=,即y=,其图象由两条抛物线的部分图形组成,图象如图3.解法二 先作函数 y = x2-4x+3 的图象,然后将其在 x 轴下方的图象翻折到 x 轴的上方,原 x 轴上方的图形及其翻折上来的图形便是所要求作的函数的图象.Oxy11图 1Oxy11图 2Oxy图 3123点评 作不熟悉的函数图象,可以先将函数式变形,化为基本初等函数的图象再作图.但要注意变形的等价性,不要扩大或缩小未知数的取值范围.例 2 设有三个函数的图象分别是 C1、C2、C3,其中函数 y=f(x)的图象是 C1,C2与 C1关于原点对称,C3与 C2关于直线 y=x 对称.(1)与图象 C3对应的函数是( );A....