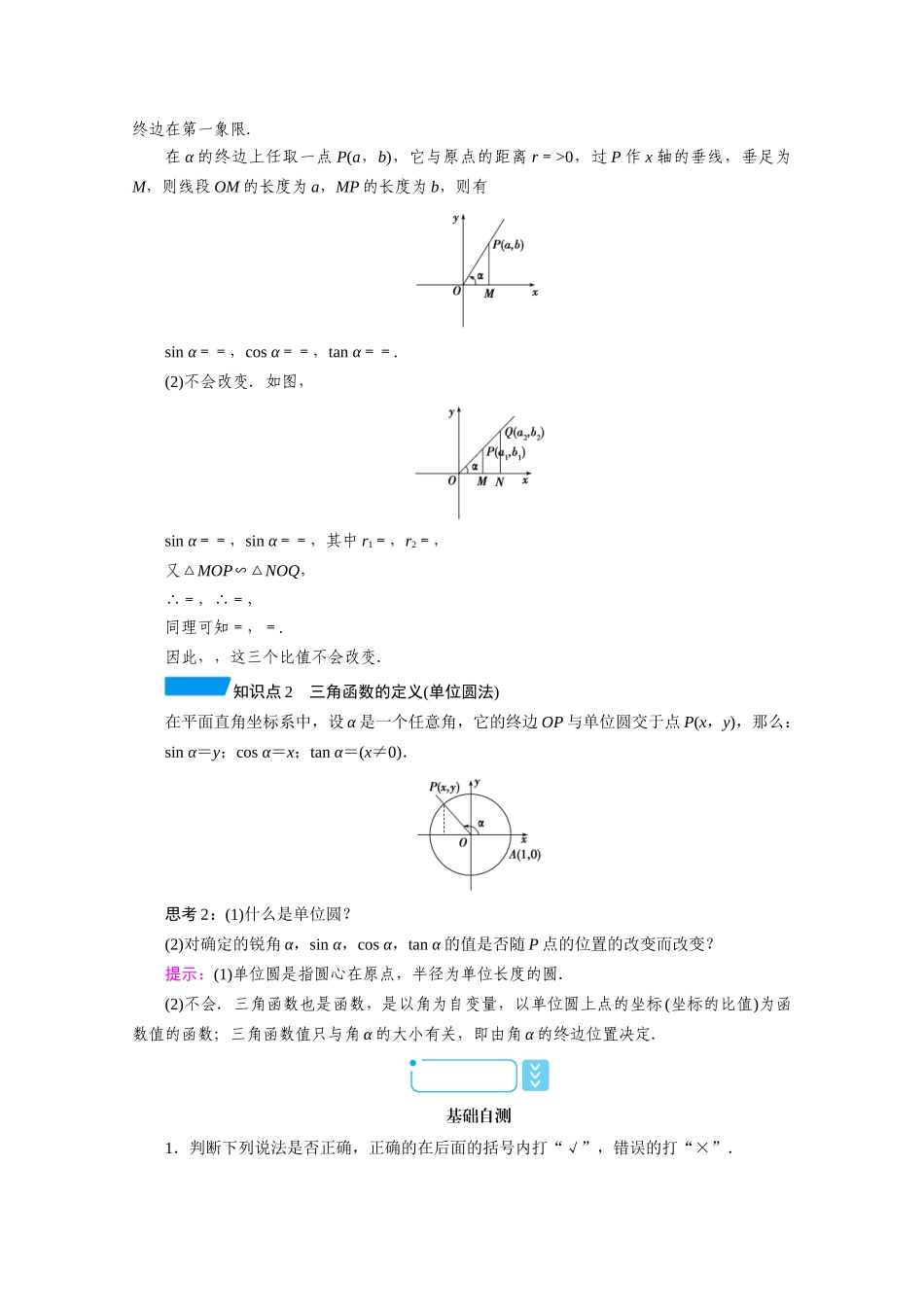
5.2 三角函数的概念5.2.1 三角函数的概念【素养目标】1.借助单位圆理解三角函数(正弦、余弦、正切)的定义.(数学建模)2.理解三角函数的概念.(数学抽象)3.熟练掌握三角函数值在各象限的符号.(直观想象)4.通过对任意角的三角函数定义的理解,掌握终边相同的角的同一三角函数值相等.(数学运算)5.通过对三角函数值的符号、诱导公式一的推导,提高学生分析、探究、解决问题的能力.(逻辑推理)【学法解读】在本节学习中利用坐标系中单位圆给出角的三角函数的定义,由三角函数定义判断出函数值符号,得出其结论“一全正、二正弦、三正切、四余弦”.第 1 课时 三角函数的概念(一) 必备知识·探新知基础知识知识点 1 三角函数的定义(坐标法)如图,设 α 是一个任意角,它的终边上任意一点 P(不与原点 O 重合)的坐标为(x,y),点P 与原点的距离为 r,则 sin α=____,cos α=____,tan α=____.我们将正弦函数、余弦函数和正切函数统称为__三角函数__,通常将它们记为:正弦函数y=sin x,x∈R;余弦函数y=cos x,x∈R;正切函数y=tan x,x≠+kπ(k∈Z).思考 1:(1)在初中是如何定义锐角三角函数的?(2)如果改变 α 终边上点 P 的位置,a,b,r 均会改变,那么,,这三个比值会改变吗?为什么?提示:(1)如图,设锐角 α 的顶点与原点 O 重合,始边与 x 轴的非负半轴重合,那么它的终边在第一象限.在 α 的终边上任取一点 P(a,b),它与原点的距离 r=>0,过 P 作 x 轴的垂线,垂足为M,则线段 OM 的长度为 a,MP 的长度为 b,则有sin α==,cos α==,tan α==.(2)不会改变.如图,sin α==,sin α==,其中 r1=,r2=,又△MOP∽△NOQ,∴=,∴=,同理可知=,=.因此,,这三个比值不会改变.知识点 2 三角函数的定义(单位圆法)在平面直角坐标系中,设 α 是一个任意角,它的终边 OP 与单位圆交于点 P(x,y),那么:sin α=y;cos α=x;tan α=(x≠0).思考 2:(1)什么是单位圆?(2)对确定的锐角 α,sin α,cos α,tan α 的值是否随 P 点的位置的改变而改变?提示:(1)单位圆是指圆心在原点,半径为单位长度的圆.(2)不会.三角函数也是函数,是以角为自变量,以单位圆上点的坐标(坐标的比值)为函数值的函数;三角函数值只与角 α 的大小有关,即由角 α 的终边位置决定.基础自测1.判断下列说法是否正确,正确的在后面的括号内打“√...