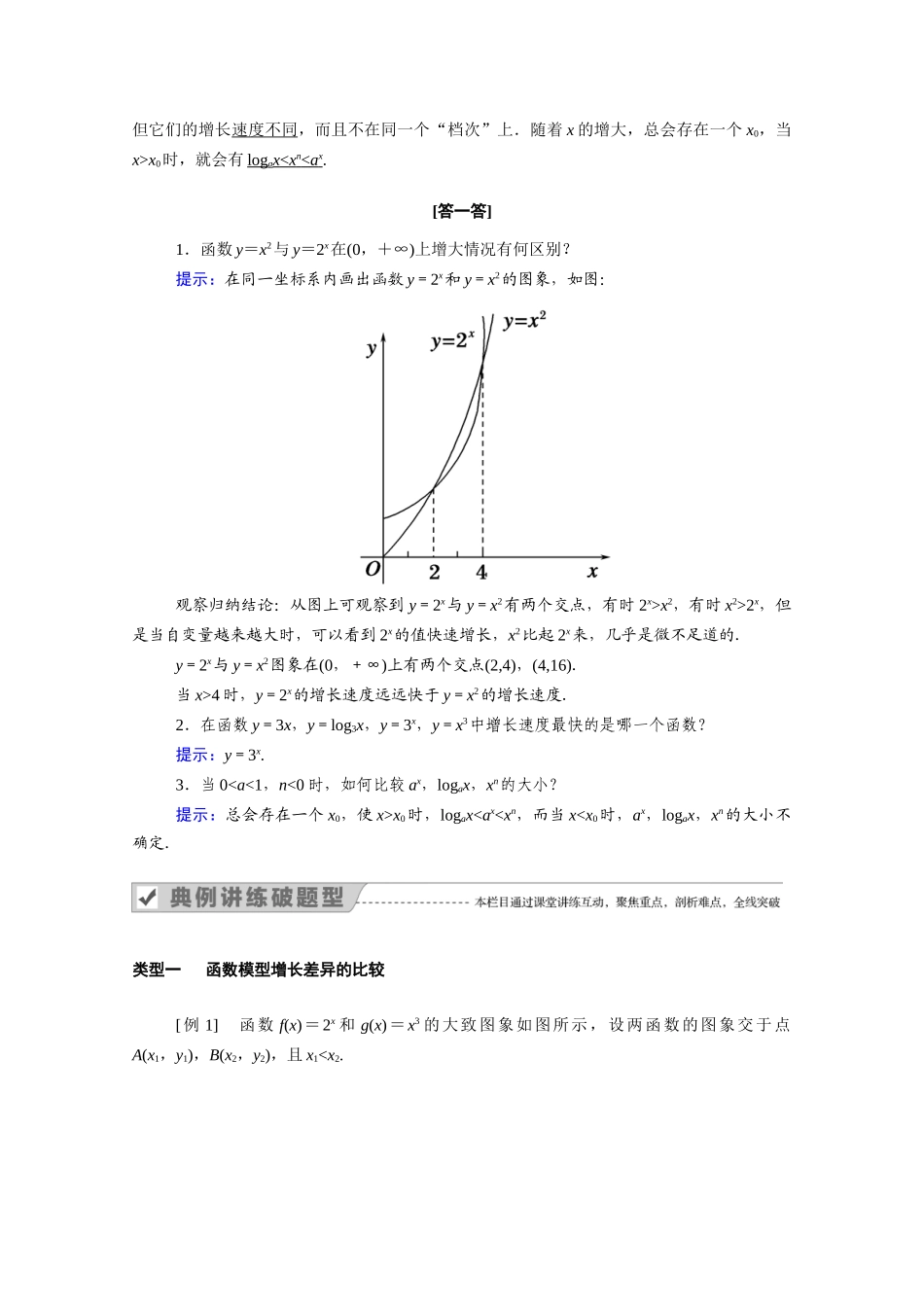
4.4.3 不同函数增长的差异[目标] 1.了解和体会函数模型在社会生活及科研中的广泛应用;2.理解直线上升、指数爆炸、对数增长的含义以及三种函数模型性质的比较;3.会分析具体的实际问题,能够建模解决实际问题.[重点] 几类不同函数模型增长的含义及差异.[难点] 如何选择数学模型分析解决实际问题.知识点 三类不同增长的函数模型的比较[填一填]1.三类函数模型的性质2.函数 y=ax(a>1),y=logax(a>1)或 y=xn(n>0)增长速度的对比(1)对于指数函数 y=ax(a>1)和幂函数 y=xn(n>0),在区间(0,+∞)上,无论 n 比 a 大多少,尽管在 x 的一定范围内,ax会小于 xn,但由于 a x 的增长 快于 x n 的增长 ,因此总存在一个x0,当 x>x0时,就会有 a x > x n .(2)对于对数函数 y=logax(a>1)和幂函数 y=xn(n>0),在区间(0,+∞)上,尽管在 x 的一定范围内,logax 可能会大于 xn,但由于 logax 的增长慢于 xn的增长,因此总存在一个 x0,当x>x0时,就会有 logax < x n .(3)在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着 x 的增大,总会存在一个 x0,当x>x0时,就会有 logax < x n < a x .[答一答]1.函数 y=x2与 y=2x在(0,+∞)上增大情况有何区别?提示:在同一坐标系内画出函数 y=2x和 y=x2的图象,如图:观察归纳结论:从图上可观察到 y=2x与 y=x2有两个交点,有时 2x>x2,有时 x2>2x,但是当自变量越来越大时,可以看到 2x的值快速增长,x2比起 2x来,几乎是微不足道的.y=2x与 y=x2图象在(0,+∞)上有两个交点(2,4),(4,16).当 x>4 时,y=2x的增长速度远远快于 y=x2的增长速度.2.在函数 y=3x,y=log3x,y=3x,y=x3中增长速度最快的是哪一个函数?提示:y=3x.3.当 0
x0时,logax