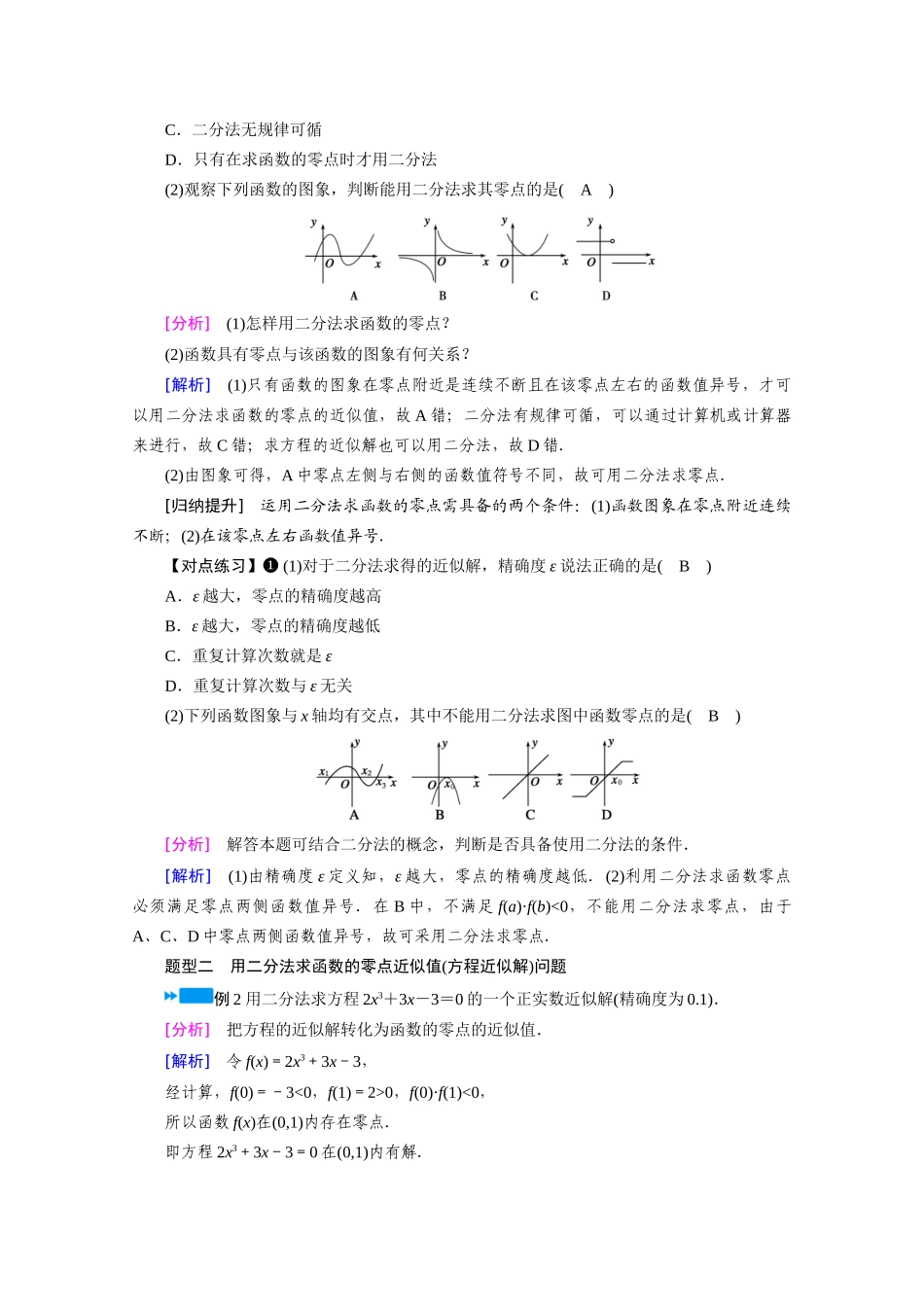
4.5.2 用二分法求方程的近似解必备知识·探新知基础知识知识点 1 二分法的概念对于在区间[a,b]上__连续不断__且__f ( a )· f ( b )<0 __的函数 y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到函数零点近似值的方法叫做二分法.思考 1:是否所有的函数都可以用二分法求函数的零点?提示:不是,只有满足函数图象在零点附近连续,且在该零点左右函数值异号时,才能应用“二分法”求函数零点.知识点 2 用二分法求函数 f(x)的零点近似值的步骤(1)确定区间[a,b],验证__f ( a )· f ( b ) < 0 __,给定精确度 ε;(2)求区间(a,b)的中点 c;(3)计算 f(c):若 f(c)=__0__,则 c 就是函数的零点;若 f(a)·f(c)__<__0,则令 b=c[此时零点 x0∈(a,c)];若 f(c)·f(b)__<__0,则令 a=c[此时零点 x0∈(c,b)].(4)判断是否达到精确度 ε:即若|a-b|__<__ε,则得到零点的近似值为 a(或 b);否则重复(2)~(4).思考 2:零点的近似解只能是区间的端点 a 或 b 吗?提示:不是,区间的端点可以,区间的中点也可以,实际上区间上的任意一个值都可以.基础自测1.以下每个图象表示的函数都有零点,但不能用二分法求函数零点近似值的是( C )[解析] 由二分法的定义,可知只有当函数 f(x)在区间[a,b]上的图象连续不断,且f(a)f(b)<0,即函数的零点是变号零点时,才能将区间[a,b]一分为二,逐步得到零点的近似值.对各选项分析可知,选项 A,B,D 都符合,而选项 C 不符合,因为在零点两侧函数值不异号,因此不能用二分法求函数零点的近似值.2.下列函数中不能用二分法求零点近似值的是( C )A.f(x)=3x-1 B.f(x)=x3C.f(x)=|x|D.f(x)=ln x[解析] 对于选项 C 而言,令|x|=0,得 x=0,即函数 f(x)=|x|存在零点,但当 x>0 时,f(x)>0,当 x<0 时,f(x)>0,所以 f(x)=|x|的函数值非负,即函数 f(x)=|x|有零点,但零点两侧函数值不异号,所以不能用二分法求零点的近似值.3.(2019·河南永城实验中学高一期末测试)用二分法求函数 f(x)=x3+5 的零点可以取的初始区间是( A )A.[-2,1]B.[-1,0]C.[0,1]D.[1,2][解析] f(-2)=(-2)3+5=-8+5=-3<0,f(1)=1+5=6>0,∴f(-2)·f(1)<0,故选 A.4.函数 f(x)的图象如图所示,则函数 f(x)的变号零点的个数为( D )A.0 B.1C.2D.3[解析] 函数 f(x...