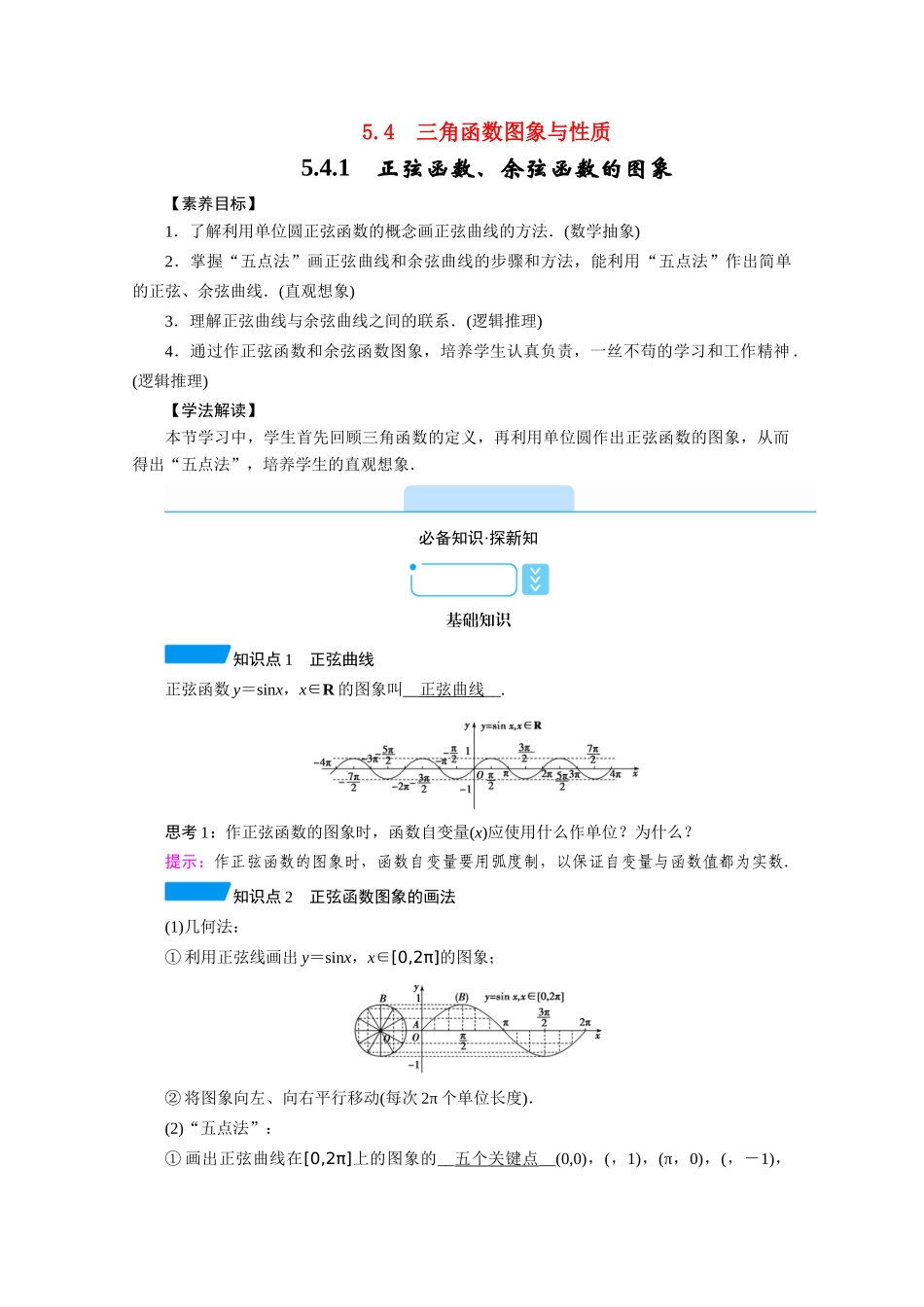
5.4 三角函数图象与性质5.4.1 正弦函数、余弦函数的图象【素养目标】1.了解利用单位圆正弦函数的概念画正弦曲线的方法.(数学抽象)2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能利用“五点法”作出简单的正弦、余弦曲线.(直观想象)3.理解正弦曲线与余弦曲线之间的联系.(逻辑推理)4.通过作正弦函数和余弦函数图象,培养学生认真负责,一丝不苟的学习和工作精神.(逻辑推理)【学法解读】本节学习中,学生首先回顾三角函数的定义,再利用单位圆作出正弦函数的图象,从而得出“五点法”,培养学生的直观想象.必备知识·探新知基础知识知识点 1 正弦曲线正弦函数 y=sinx,x∈R 的图象叫__正弦曲线__.思考 1:作正弦函数的图象时,函数自变量(x)应使用什么作单位?为什么?提示:作正弦函数的图象时,函数自变量要用弧度制,以保证自变量与函数值都为实数.知识点 2 正弦函数图象的画法(1)几何法:① 利用正弦线画出 y=sinx,x∈[0,2π]的图象;② 将图象向左、向右平行移动(每次 2π 个单位长度).(2)“五点法”:① 画出正弦曲线在[0,2π]上的图象的__五个关键点__(0,0),(,1),(π,0),(,-1),(2π,0),用光滑的曲线连接;② 将所得图象向左、向右平行移动(每次 2π 个单位长度).思考 2:观察上图,你认为正弦曲线是如何画出来的?提示:利用单位圆中的正弦线可以作出 y=sinx,x∈[0,2π]的图象,将 y=sinx 在[0,2π]内的图象左右平移即可得到正弦曲线.知识点 3 余弦曲线余弦函数 y=cosx,x∈R 的图象叫余弦曲线.思考 3:你认为应该利用正弦函数和余弦函数的哪些关系,通过怎样的图形变换,才能将正弦函数的图象变换为余弦函数的图象?提示:诱导公式 左右平移知识点 4 余弦函数图象的画法(1)要得到 y=cosx 的图象,只需把 y=sinx 的图象向左平移个单位长度即可,这是由于cosx=sin(x+).(2)用“五点法”:画余弦函数 y=cosx 在[0,2π]上的图象时,所取的五个关键点分别为(0,1),(,0),(π,-1),(,0),(2π,1),再用光滑的曲线连接.思考 4:正弦曲线和余弦曲线有怎样的关系?提示:基础自测1.对于正弦函数 y=sinx 的图象,下列说法错误的是( D )A.过原点B.与 y=cosx 的图象形状相同,只是位置不同C.与 x 轴有无数个交点D.关于 y 轴对称2.从函数 y=cosx,x∈[0,2π)的图象来看,满足 cosx=的 x 有( B )A.1 个值 B.2 个值C.3 个值D.4 ...