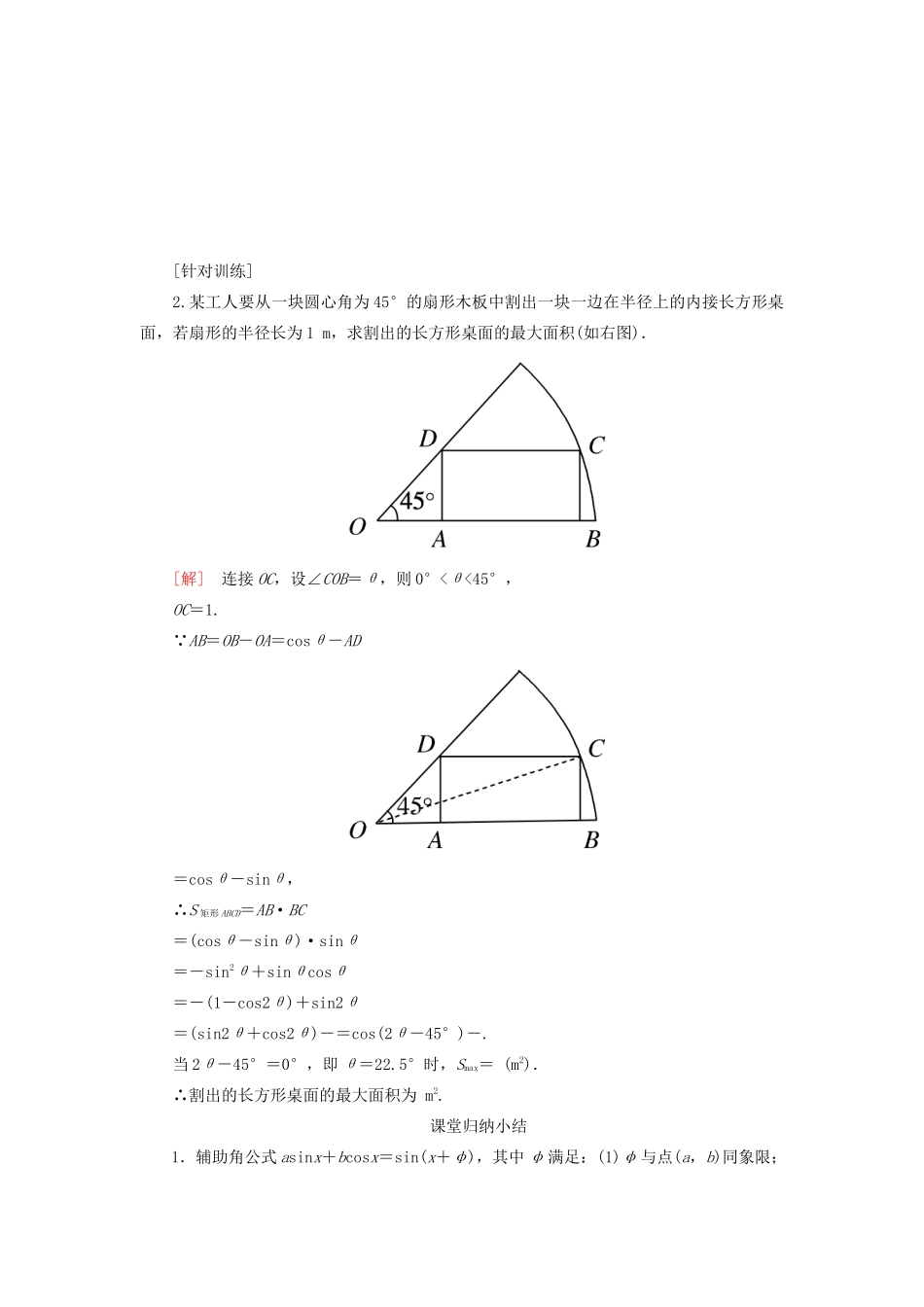
第 2 课时 三角恒等变换的应用题型一 三角恒等变换与三角函数性质的综合 【典例 1】 已知函数 f(x)=sin+2sin2(x∈R).(1)求函数 f(x)的最小正周期;(2)求使函数 f(x)取得最大值的 x 的集合.[思路导引] 先降幂,再用辅助角公式化为 Asin(ωx+φ)的形式,从而研究三角函数的性质.[解] (1) f(x)=sin+2sin2=sin+1-cos=2+1=2sin+1=2sin+1,∴f(x)的最小正周期为 T==π.(2)当 f(x)取得最大值时,sin=1,有 2x-=2kπ+,即 x=kπ+(k∈Z),∴所求 x 的集合为.(1)为了研究函数的性质,往往要充分利用三角变换公式转化为正弦型(余弦型)函数,这是解决问题的前提.(2)解此类题时要充分运用两角和(差)、二倍角公式、辅助角转换公式消除差异,减少角的种类和函数式的项数,为讨论函数性质提供保障.[针对训练]1.已知函数 f(x)=2sin(x-3π)·sin+2sin2-1,x∈R.(1)求函数 f(x)的最小正周期及在区间上的最大值和最小值;(2)若 f(x0)=,x0∈,求 cos2x0的值.[解] f(x)=(2sinxcosx)+(2cos2x-1)=sin2x+cos2x=2sin.(1)f(x)的最小正周期为 π;最大值为 2,最小值为-1.(2)由(1)可知 f(x0)=2sin.又 f(x0)=,∴sin=.由 x0∈,得 2x0+∈,∴cos=-=-,cos2x0=cos=coscos+sinsin=.题型二三角恒等变换在实际生活中的应用【典例 2】 有一块以 O 为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD 开辟为绿地,使其一边 AD 落在半圆的直径上,另外两点 B,C 落在半圆的圆周上,已知半圆的半径长为 a,如何选择关于点 O 对称的点 A,D 的位置,可以使矩形 ABCD 的面积最大?[思路导引] 在△AOB 中利用∠AOB 表示 OA,AB 的长,然后表示出矩形面积:2OA·OB,从而得到面积与角间的函数关系,再通过求函数的最值得到面积的最值.[解] 画出图象如右图所示,设∠AOB=θ,则 AB=asinθ,OA=acosθ.设矩形 ABCD 的面积为 S,则 S=2OA·AB,即 S=2acosθ·asinθ=a2·2sinθcosθ=a2sin2θ. θ∈,∴2θ∈(0,π),当 2θ=,即 θ=时,Smax=a2,此时,A,D 距离 O 点都为a.解决实际问题应首先设定主变量角 α 以及相关的常量与变量,建立含有角 α 的三角函数关系式,再利用三角函数的变换、性质等进行求解.求三角函数最值的问题,一般需利用三角函数的有界性来解决.[针对训练]2.某工人要从一块圆心角为 45°的扇形木板中割出一块一边在...