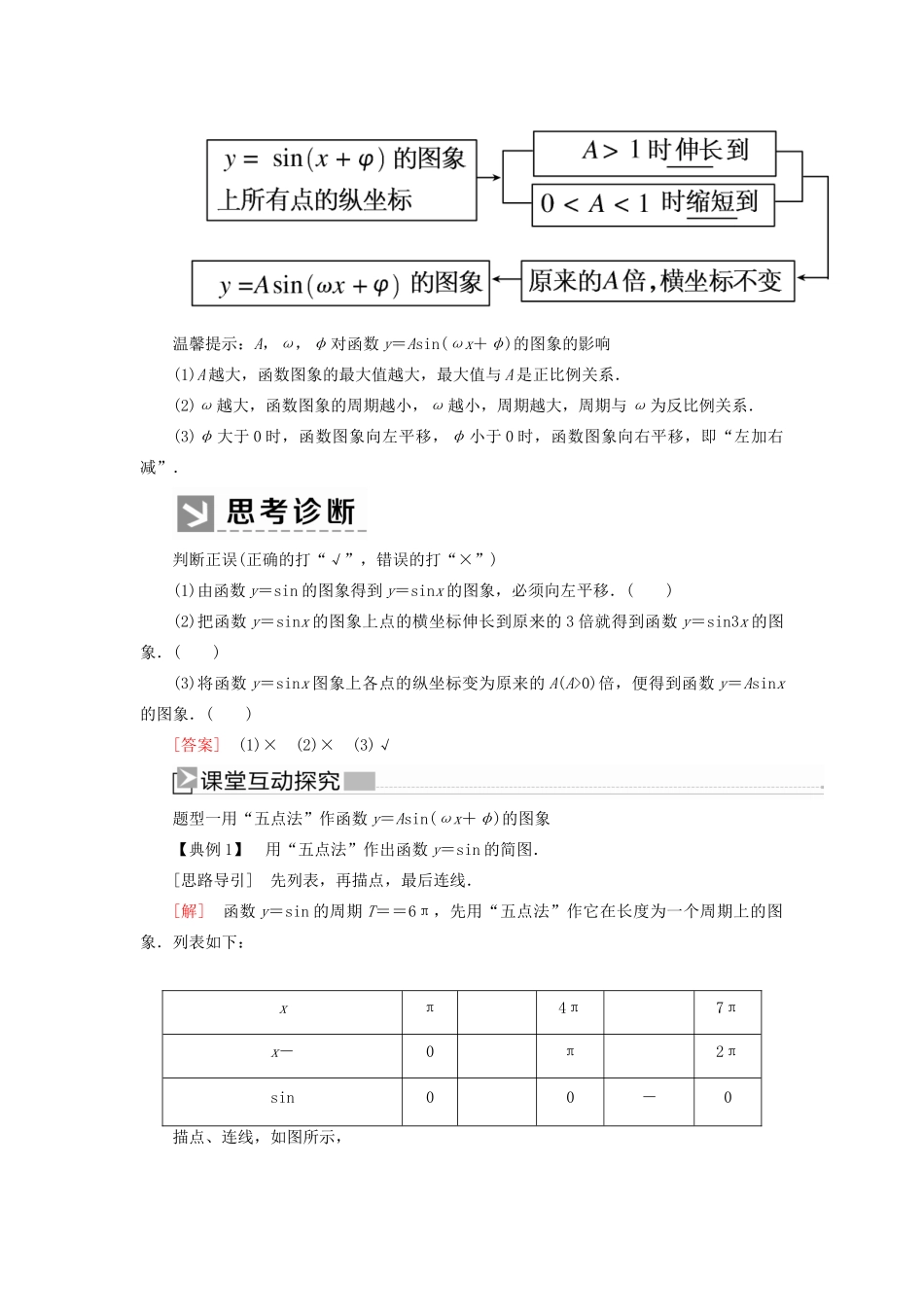
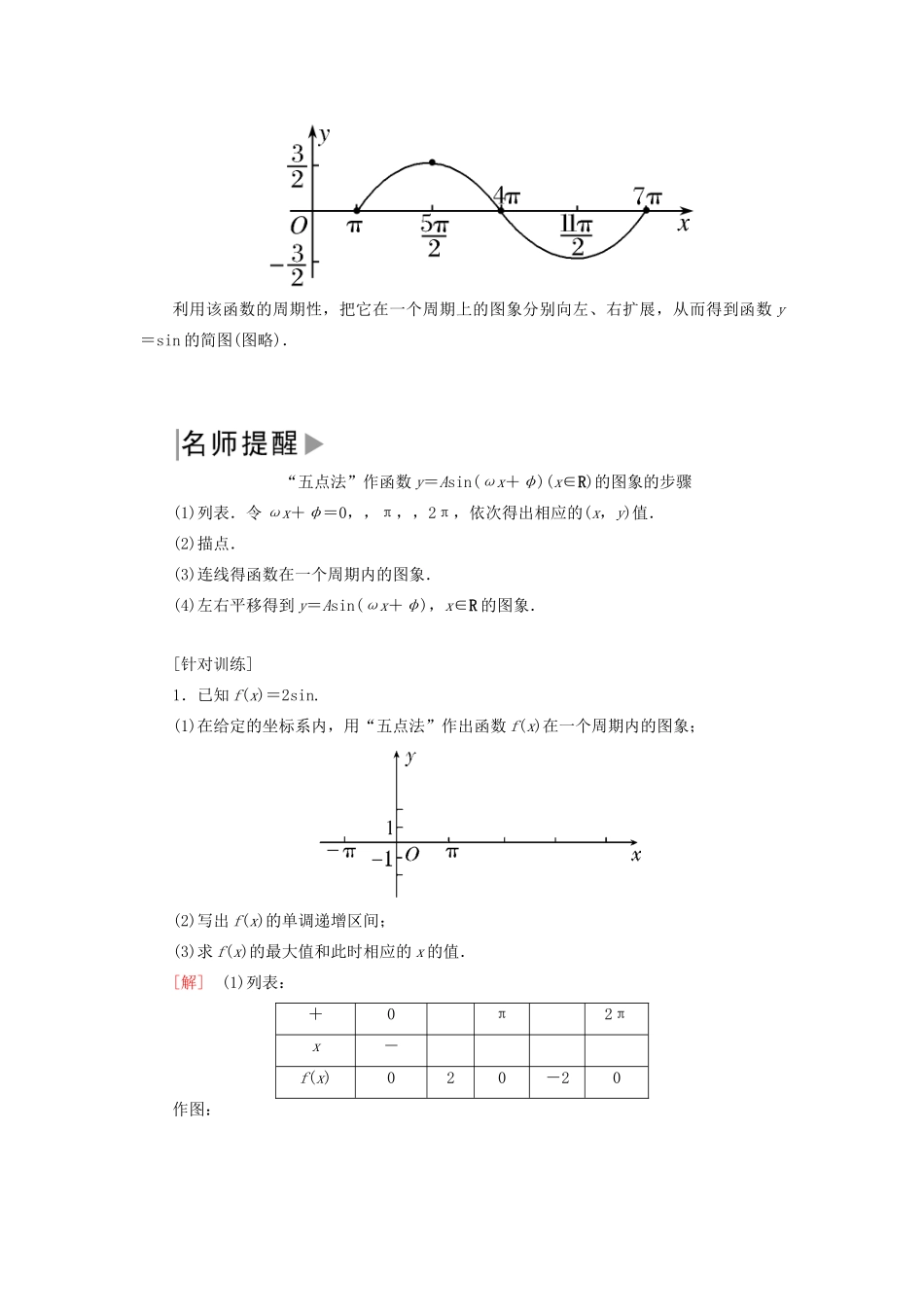
第 1 课时 函数 y=Asin(ωx+φ)的图象(一)1.会用“五点法”画函数 y=Asin(ωx+φ)的图象.2.理解 y=Asin(ωx+φ)中 ω、φ、A 对图象的影响.3.掌握 y=sinx 与 y=Asin(ωx+φ)图象间的变换关系,并能正确地指出其变换步骤. 参数 A、ω、φ 对函数 y=Asin(ωx+φ)的图象的影响(1)φ 对函数 y=sin(x+φ),x∈R 的图象的影响(2)ω(ω>0 且 ω≠1)对 y=sin(ωx+φ)的图象的影响(3)A(A>0 且 A≠1)对 y=Asin(ωx+φ)的图象的影响温馨提示:A,ω,φ 对函数 y=Asin(ωx+φ)的图象的影响(1)A 越大,函数图象的最大值越大,最大值与 A 是正比例关系.(2)ω 越大,函数图象的周期越小,ω 越小,周期越大,周期与 ω 为反比例关系.(3)φ 大于 0 时,函数图象向左平移,φ 小于 0 时,函数图象向右平移,即“左加右减”.判断正误(正确的打“√”,错误的打“×”)(1)由函数 y=sin 的图象得到 y=sinx 的图象,必须向左平移.( )(2)把函数 y=sinx 的图象上点的横坐标伸长到原来的 3 倍就得到函数 y=sin3x 的图象.( )(3)将函数 y=sinx 图象上各点的纵坐标变为原来的 A(A>0)倍,便得到函数 y=Asinx的图象.( )[答案] (1)× (2)× (3)√题型一用“五点法”作函数 y=Asin(ωx+φ)的图象 【典例 1】 用“五点法”作出函数 y=sin 的简图.[思路导引] 先列表,再描点,最后连线.[解] 函数 y=sin 的周期 T==6π,先用“五点法”作它在长度为一个周期上的图象.列表如下:xπ4π7πx-0π2πsin00-0描点、连线,如图所示,利用该函数的周期性,把它在一个周期上的图象分别向左、右扩展,从而得到函数 y=sin 的简图(图略). “五点法”作函数 y=Asin(ωx+φ)(x∈R)的图象的步骤(1)列表.令 ωx+φ=0,,π,,2π,依次得出相应的(x,y)值.(2)描点.(3)连线得函数在一个周期内的图象.(4)左右平移得到 y=Asin(ωx+φ),x∈R 的图象.[针对训练]1.已知 f(x)=2sin.(1)在给定的坐标系内,用“五点法”作出函数 f(x)在一个周期内的图象;(2)写出 f(x)的单调递增区间;(3)求 f(x)的最大值和此时相应的 x 的值.[解] (1)列表:+0π2πx-f(x)020-20作图:(2)由 2kπ-≤+≤2kπ+,得 4kπ-≤x≤4kπ+,k∈Z.所以函数 f(x)的单调递增区间为,k∈Z.(3)当+=+2kπ,即 x=+4kπ(k∈Z)时,f(x)max=2.题型二函数图象的平移变...