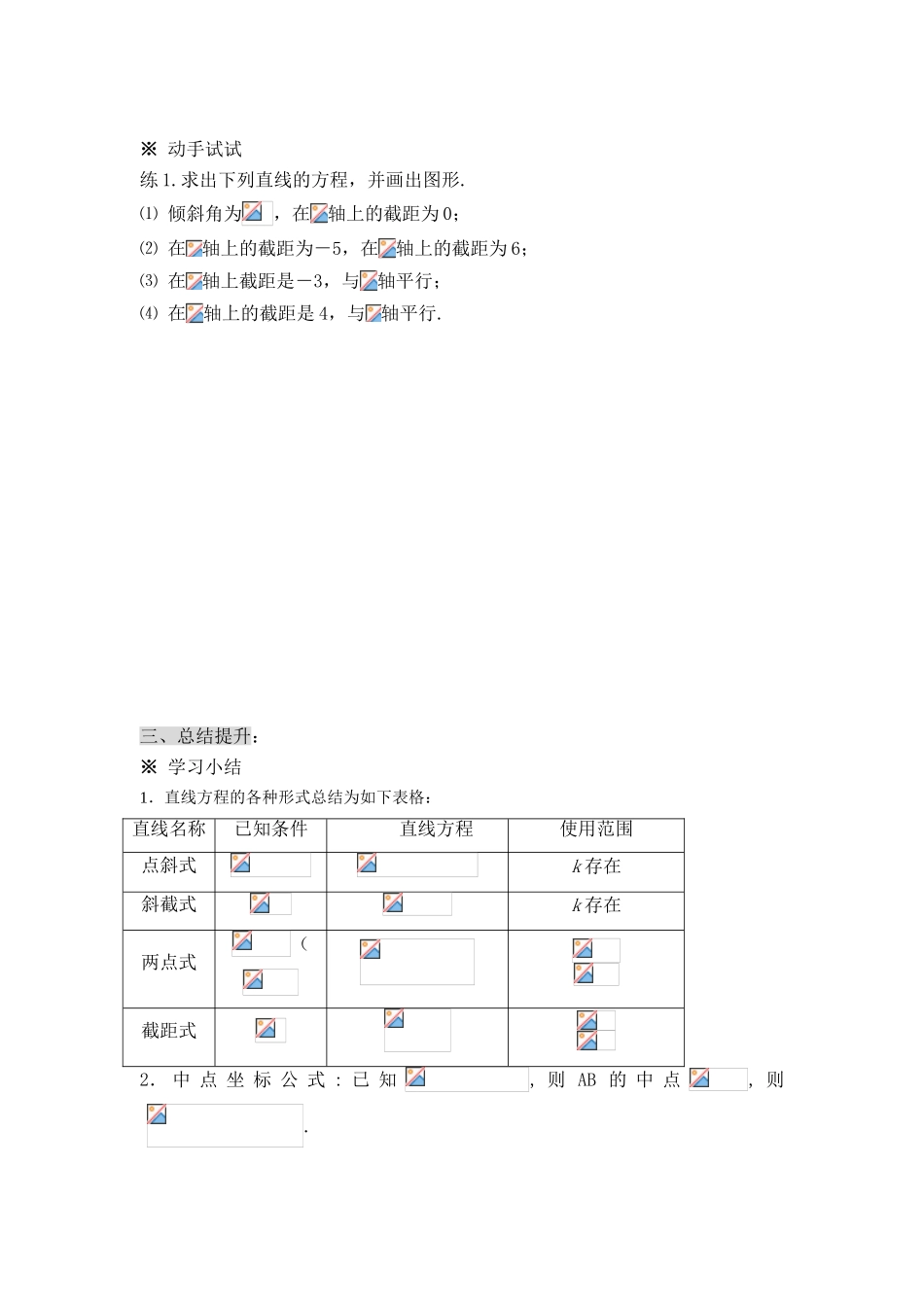
直线的两点式方程 学习目标 1.掌握直线方程的两点的形式特点及适用范围;2.了解直线方程截距式的形式特点及适用范围. 学习重点 直线方程两点式。 学习难点 两点式推导过程的理解。 学习过程 一、课前准备:(预习教材 P73~ P74,找出疑惑之处)复习 1:直线过点,斜率是 1,则直线方程为 ;直线的倾斜角为,纵截距为,则直线方程为 .2.方程表示过点 ,斜率是 ,倾斜角是 ,在 y 轴上的截距是 的直线.3.已知直线 经过两点,求直线 的方程.二、新课导学:※ 学习探究新知 1:已知直线上两点且,则通过这两点的直线方程为 ,由于这个直线方程由两点确定,所以我们把它叫直线的两点式方程,简称两点式.问题 1:哪些直线不能用两点式表示?例 已知直线过,求直线的方程并画出图象.新知 2:已知直线与轴的交点为,与轴的交点为,其中,则直线 的方程 叫做直线的截距式方程 .注意:直线与轴交点(,0)的横坐标叫做直线在轴上的截距;直线与 y轴交点(0,)的纵坐标叫做直线在轴上的截距.问题 3:,表示截距,是不是表示直线与坐标轴的两个交点到原点的距离?问题 4:到目前为止,我们所学过的直线方程的表达形式有多少种?它们之间有什么关系?※ 典型例题例 1 求过下列两点的直线的两点式方程,再化为截距式方程.⑴;⑵.例 2 已知三角形的三个顶点,,求边所在直线的方程,以及该边上中线所在直线的方程.※ 动手试试练 1.求出下列直线的方程,并画出图形.⑴ 倾斜角为,在轴上的截距为 0;⑵ 在轴上的截距为-5,在轴上的截距为 6;⑶ 在轴上截距是-3,与轴平行;⑷ 在轴上的截距是 4,与轴平行.三、总结提升:※ 学习小结1.直线方程的各种形式总结为如下表格:直线名称已知条件直线方程使用范围点斜式k 存在斜截式k 存在两点式(截距式2. 中 点 坐 标 公 式 : 已 知, 则 AB 的 中 点, 则. 学习评价 ※ 当堂检测:1. 直线 过点两点,点在 上,则 的值为 .2. 若直线通过第二、三、四象限,则系数需满足条件 . 3. 直线()的图象是( ) 4. 在轴 上 的 截 距 为 2 , 在轴 上 的 截 距 为的 直 线 方 程 .5. 直线关于 轴对称的直线方程 ,关于轴对称的 直 线 方 程 关 于 原 点 对 称 的 方 程 . 课后作业 1. 过点 P(2,1)作直线 交正半轴于 AB 两点,当取到最小值时,求直线 的方程.2. 已知一直线被两直线,:截得的线段的中点恰好是坐标原点,求该直线方程.