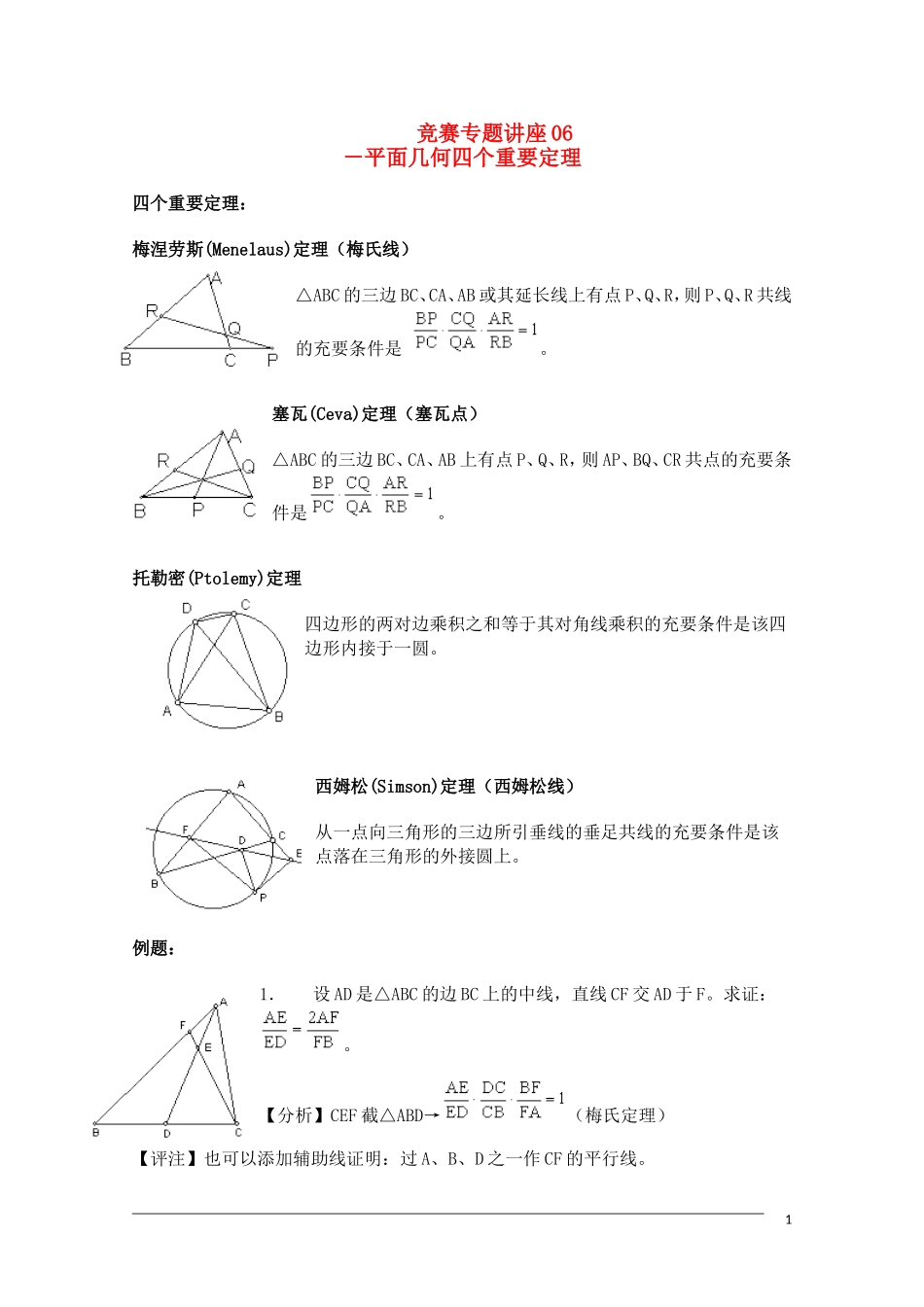
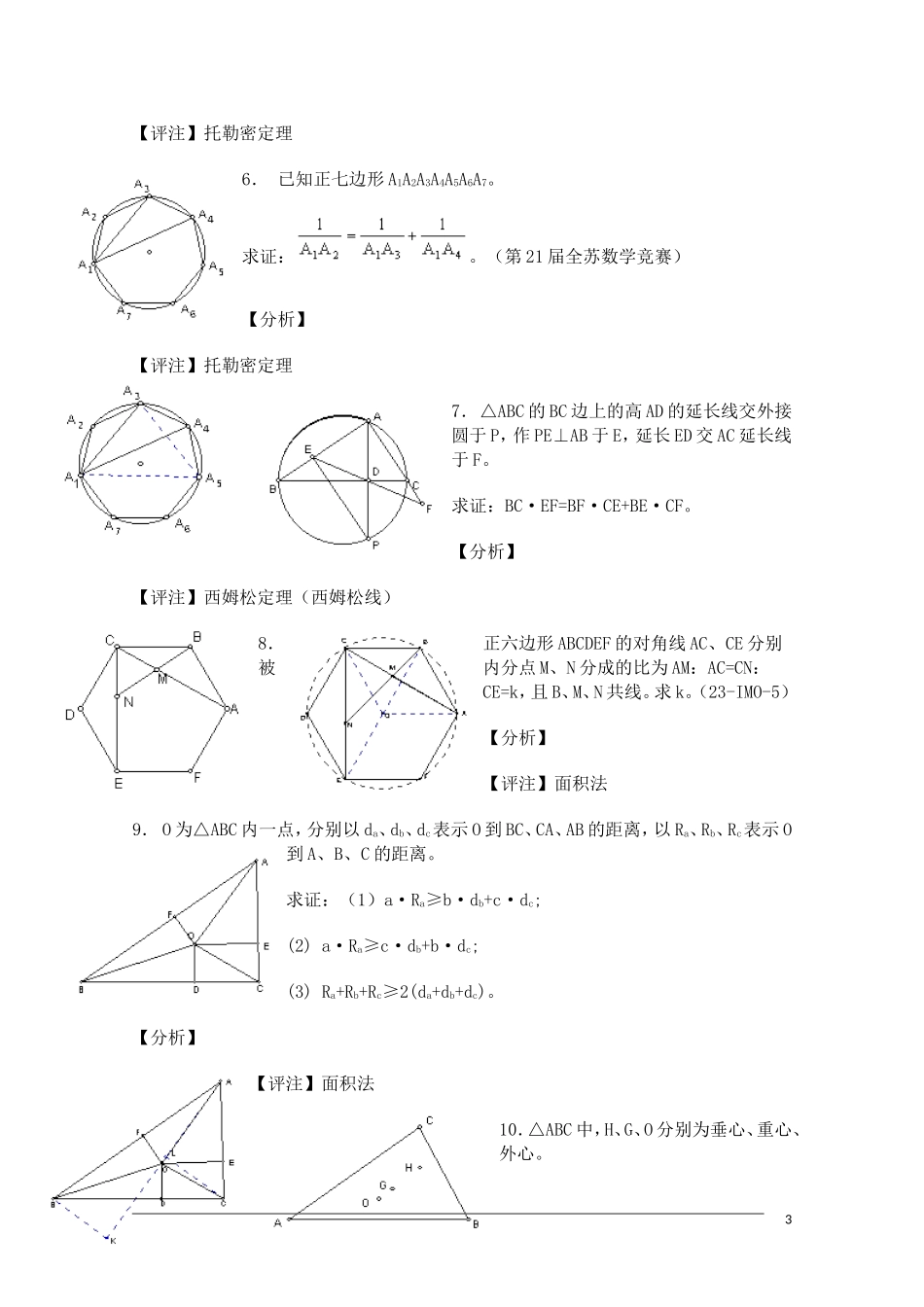
竞赛专题讲座 06-平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边 BC、CA、AB 或其延长线上有点 P、Q、R,则 P、Q、R 共线的充要条件是 。塞瓦(Ceva)定理(塞瓦点)△ABC 的三边 BC、CA、AB 上有点 P、Q、R,则 AP、BQ、CR 共点的充要条件是。托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。例题:1. 设 AD 是△ABC 的边 BC 上的中线,直线 CF 交 AD 于 F。求证:。【分析】CEF 截△ABD→(梅氏定理)【评注】也可以添加辅助线证明:过 A、B、D 之一作 CF 的平行线。12. 过△ABC 的重心 G 的直线分别交 AB、AC 于 E、F,交 CB于 D。求证:。【分析】连结并延长 AG交BC 于 M,则 M 为 BC 的中点。DEG 截△ABM→(梅氏定理)DGF 截△ACM→(梅氏定理)∴===1【评注】梅氏定理3. D、E、F 分别在△ABC 的 BC、CA、AB 边上,,AD、BE、CF 交成△LMN。求 S△LMN。【分析】【评注】梅氏定理4. 以△ABC 各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证:AE、BF、CG 相交于一点。【分析】【评注】塞瓦定理5. 已知△ABC 中,∠B=2∠C。求证:AC2=AB2+AB·BC。【分析】过 A 作 BC 的平行线交△ABC 的外接圆于 D,连结 BD。则CD=DA=AB,AC=BD。由托勒密定理,AC·BD=AD·BC+CD·AB。2【评注】托勒密定理6. 已知正七边形 A1A2A3A4A5A6A7。求证:。(第 21 届全苏数学竞赛)【分析】【评注】托勒密定理7. △ABC 的 BC 边上的高 AD 的延长线交外接圆于 P,作 PE⊥AB 于 E,延长 ED 交 AC 延长线于 F。求证:BC·EF=BF·CE+BE·CF。【分析】【评注】西姆松定理(西姆松线)8. 正六边形 ABCDEF 的对角线 AC、CE 分别被内分点 M、N 分成的比为 AM:AC=CN:CE=k,且 B、M、N 共线。求 k。(23-IMO-5)【分析】【评注】面积法9. O 为△ABC 内一点,分别以 da、db、dc表示 O 到 BC、CA、AB 的距离,以 Ra、Rb、Rc表示 O到 A、B、C 的距离。求证:(1)a·Ra≥b·db+c·dc; (2) a·Ra≥c·db+b·dc;(3) Ra+Rb+Rc≥2(da+db+dc)。【分析】【评注】面积法10.△ABC 中,H、G、O 分别为垂心、重心、外心。3求证:H、G、O 三点共线,且 HG...