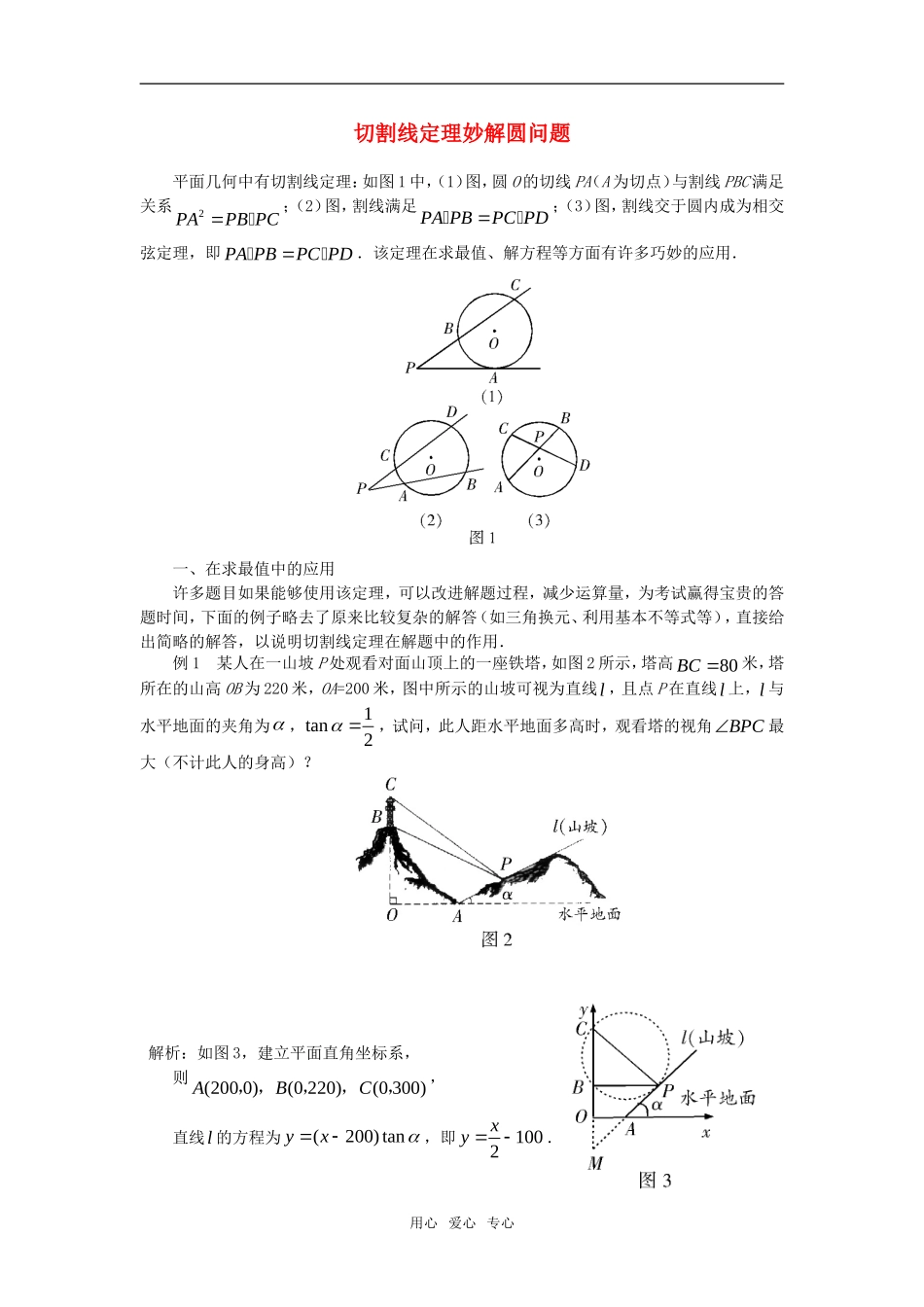
切割线定理妙解圆问题 平面几何中有切割线定理:如图 1 中,(1)图,圆 O 的切线 PA(A 为切点)与割线 PBC 满足关系2PAPB PC;(2)图,割线满足 PA PBPC PD;(3)图,割线交于圆内成为相交弦定理,即 PA PBPC PD.该定理在求最值、解方程等方面有许多巧妙的应用.一、在求最值中的应用 许多题目如果能够使用该定理,可以改进解题过程,减少运算量,为考试赢得宝贵的答题时间,下面的例子略去了原来比较复杂的解答(如三角换元、利用基本不等式等),直接给出简略的解答,以说明切割线定理在解题中的作用. 例 1 某人在一山坡 P 处观看对面山顶上的一座铁塔,如图 2 所示,塔高80BC 米,塔所在的山高 OB 为 220 米,OA=200 米,图中所示的山坡可视为直线l ,且点 P 在直线l 上,l 与水平地面的夹角为 ,1tan2 ,试问,此人距水平地面多高时,观看塔的视角BPC最大(不计此人的身高)? 解析:如图 3,建立平面直角坐标系,则(200 0)(0 220)(0 300)ABC,,,,,, 直线l 的方程为(200) tanyx,即1002xy .用心 爱心 专心 延长 PABO,交于点 M ,则由200OA ,1tan2 , 可得 OM=100,MB=320,MC=400. 由切割线定理,视角∠BPC 最大只需经过 B、C 作一个圆与直线l 相切于点 P ,则2MPMB MC,160 5MP ,又因为100 5MA ,则60 5AP ,易得此人距水平地面 60 米高时,观看塔的视角∠BPC 最大. 二、在求交点中的应用 例 2 已知( )(2005)(2006)f xxx的图象与 x 轴、y 轴有三个不同的交点,有一个圆恰好经过这三个点,则此圆与坐标轴的另一个交点的坐标是( ) A.(01),B.(0 2),C.200502006,D.200602005, 解析:如图 4,常规方法是设出圆的一般方程,由圆心在直线12x 上,得1D ;由圆过三点(2005 0) ( 2006 0) (02005 2006),,,,,,得22(2005 2006 1)2005 20060xyxy .令0x 解 方 程2(2005 2006 1)2005 20060yy ,得1y 或2005 2006y .故选(A). 若利用相交弦定理:OA OBOCOD, 由于 A、B、D 三点的坐标分别是 (2005 0) ( 2006 0) (02005 2006),,,,,,可求出1OC , 所以此圆与坐标轴的另一个交点的坐标是(0,1),故选(A). 作为选择题,最忌讳小题大做,注意应用切割线定理或逆用切割线定理可快速解决问题.用心 爱心 专心