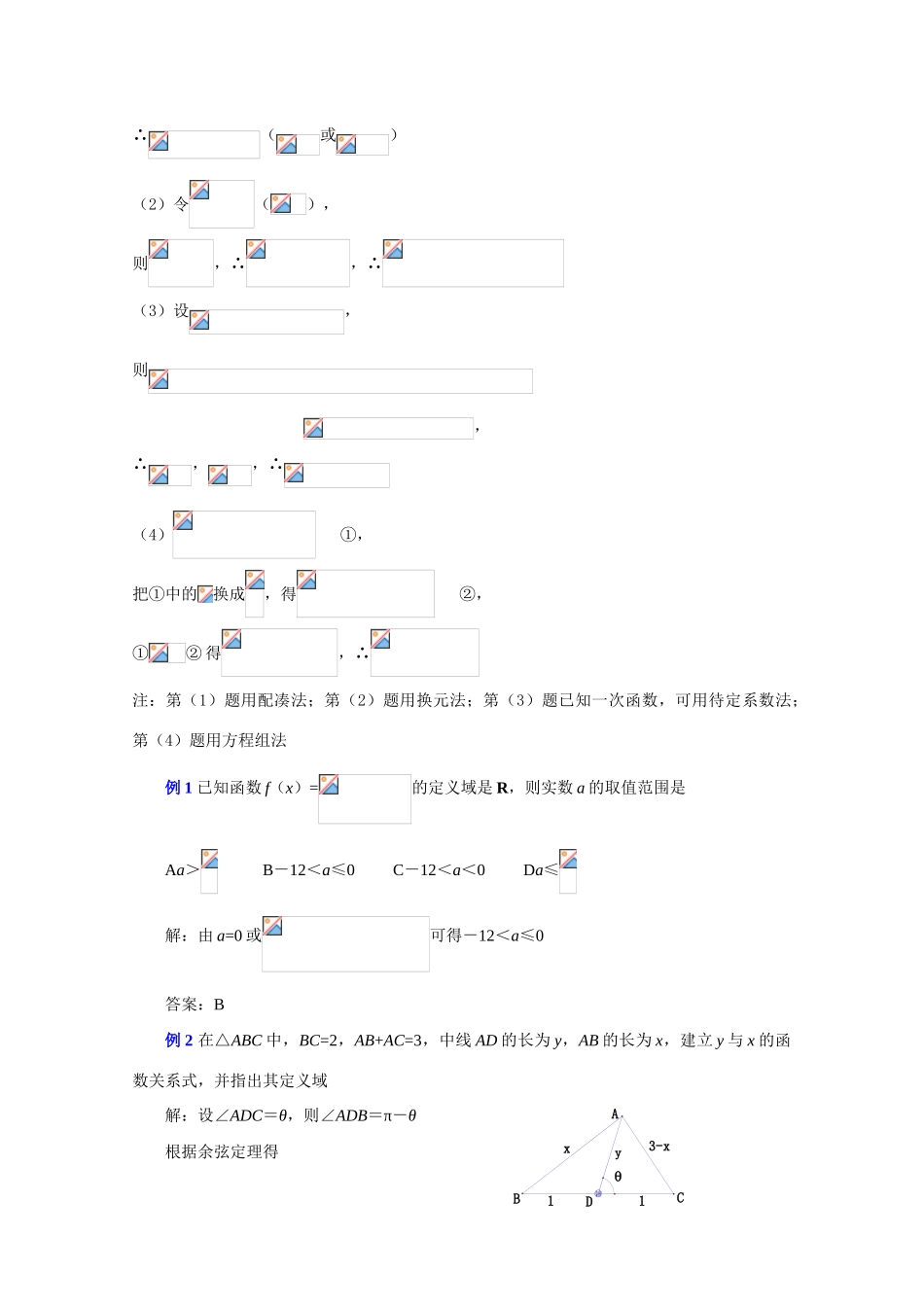
题目 第二章函数函数的解析式与表示方法高考要求 1 由所给函数表达式正确求出函数的定义域;2 掌握求函数值域的几种常用方法;3 能根据函数所具有的某些性质或它所满足的一些关系,求出它的解析式;4 会进行函数三种表示方法的互化,培养学生思维的严密性、多样性知识点归纳1 函数的三种表示法(1)解析法:就是把两个变量的函数关系,用一个等式来表示,这个等式叫做函数的解析表达式,简称解析式(2)列表法:就是列出表格来表示两个变量的函数关系(3)图象法:就是用函数图象表示两个变量之间的关系2 求函数解析式的题型有:(1)已知函数类型,求函数的解析式:待定系数法;(2)已知求或已知求:换元法、配凑法;(3)已知函数图像,求函数解析式;(4)满足某个等式,这个等式除外还有其他未知量,需构造另个等式解方程组法;(5)应用题求函数解析式常用方法有待定系数法等题型讲解 例 1(1)已知,求;(2)已知,求;(3)已知是一次函数,且满足,求;(4)已知满足,求解:(1) ,∴(或)(2)令(),则,∴,∴(3)设,则,∴,,∴(4) ①,把①中的换成,得 ②,①② 得,∴注:第(1)题用配凑法;第(2)题用换元法;第(3)题已知一次函数,可用待定系数法;第(4)题用方程组法例 1 已知函数 f(x)=的定义域是 R,则实数 a 的取值范围是Aa>B-12<a≤0C-12<a<0Da≤解:由 a=0 或可得-12<a≤0答案:B例 2 在△ABC 中,BC=2,AB+AC=3,中线 AD 的长为 y,AB 的长为 x,建立 y 与 x 的函数关系式,并指出其定义域解:设∠ADC=θ,则∠ADB=π-θ根据余弦定理得3-xyx11DCBA12+y2-2ycosθ=(3-x)2, ①12+y2-2ycos(π-θ)=x2 ②由①+②整理得 y=其中 解得<x<∴函数的定义域为(,)评述:函数的定义域是使式子有意义的自变量的取值范围,同时也要注意变量的实际意义的要求例 3 若函数 f(x)=的值域为[-1,5],求实数 a、c解:由 y=f(x)=,得 x2y-ax+cy-1=0当 y=0 时,ax=-1,∴a≠0当 y≠0 时, x∈R,∴Δ=a2-4y(cy-1)≥0∴4cy2-4y-a2≤0 -1≤y≤5,∴-1、5 是方程 4cy2-4y-a2=0 的两根∴∴评述:求 f(x)=(a12+a22≠0)的值域时,常利用函数的定义域非空这一隐含的条件,将函数转化为方程,利用 Δ≥0 转化为关于函数值的不等式求解时,要注意二次项系数为字母时要讨论例 4 设定义在 N 上的函数 f(x)满足f(...