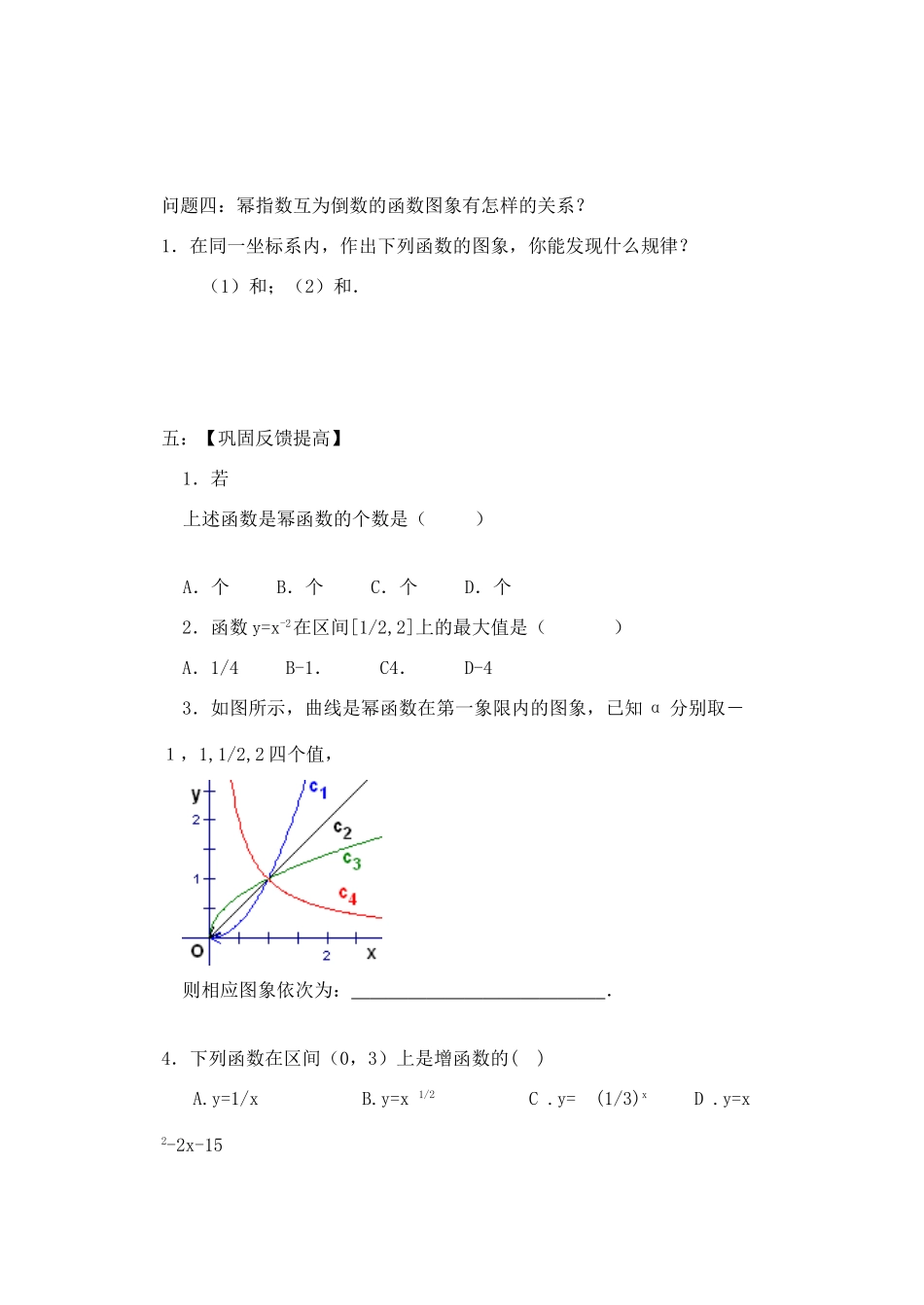
幂函数学案一. 【课标要求】① 了解幂函数的概念.② 结合函数 y=x,y=x2 ,y=x3,y=1/x,y=x1/2的图象,了解它们的变化情况.二.【学法指导】1.考察以下函数 y=x,y=x2 ,y=x3,y=1/x,y=x1/2这些函数的表达式有什么共同特征?这类函数表达式的一般形式应如何表示?请在同一个坐标系下作出这五个函数的图像。2.对于幂函数函数的探究,采用“数形结合”的方式通过对具体图象研究,让形式的认识由感性上升到理性,由特殊到一般归纳出幂函数的性质.3..幂函数性质归纳.(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);(2)时,幂函数的图象通过原点,并且在区间上是增函数.特别地,当时,幂函数的图象下凸;当时,幂函数的图象上凸;(3)时,幂函数的图象在区间上是减函数.在第一象限内,当从右边趋向原点时,图象在轴右方无限地逼近轴正半轴,当趋于时,图象在轴上方无限地逼近轴正半轴.4.思考:1.幂函数与指数函数的不同点主要表现在哪些方面?2.幂函数,x[0,+), >1 与 0<<1 的图象有何不同?3 幂函数中,如果是正偶数,这一类函数具有哪些性质?如果是正奇数呢?三.【预习检测】1.一般的,形如_______________,的函数称为幂函数,其中 α 为常数。2.(1)所有的幂函数在_________都有定义,并且图象都过点________;(2)α>0 时,幂函数的图象通过___________,并且在区间上是_________.特别地,当 α>1 时,幂函数的图象________;当 0<α<1 时,幂函数的图象_____________;(3)当 α<0 时,幂函数的图象在区间上是____________.在第一象限内,当从右边趋向原点时,图象在轴右方无限地逼近______________,当趋于时,图象在轴上方无限地逼近_________________.四.【重点难点突破】问题一:如何区别幂函数,指数函数,对数函数?1. 在函数,y=2x ,y=1/x2,y=2x2,y=x2+x,y=1,y=log2 x 中,幂函数的个数为───────问题二:类比前面讨论的指数函数,对数函数性质的思路,你能找出研究幂函数性质的方法和内容吗?1.利用幂函数的性质,比较下列各题中两个幂的值的大小:(1),; (2),;(3),; (4),. 问题三:如何研究具体函数的性质1.作出函数 y=x3/2的图象,根据图象讨论这个函数有哪些性质,并给出证明。 2.作出函数 y=x-2和函数 y=(x-3)-2的图象,求这两个函数的定义域和单调区间,并观察这两个函数图像之间的关系。 问题四:幂指数互为倒数的函数图象有怎样的...