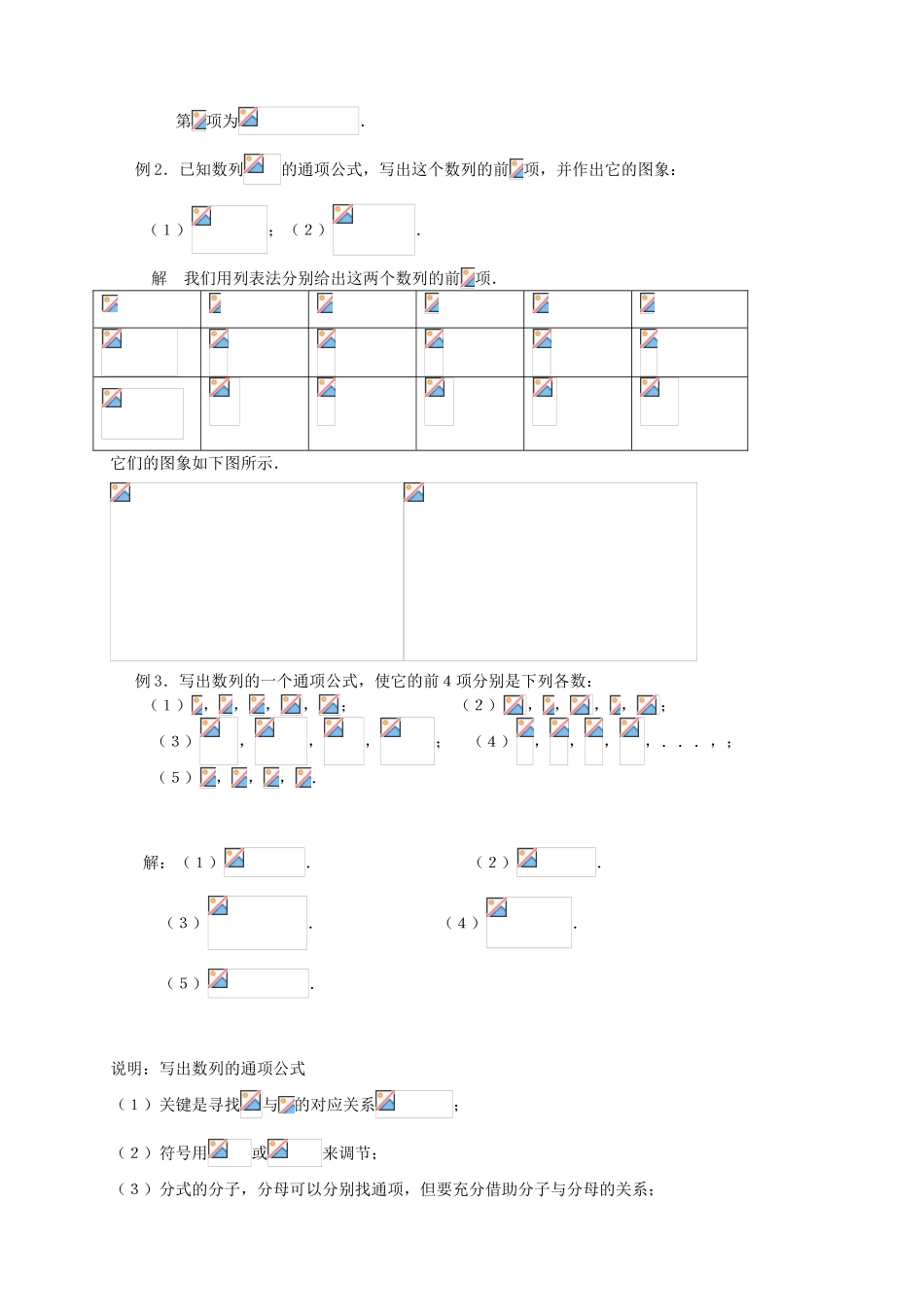
§2.1 第 1 课时 数列(1)教学目标(1)了解数列的概念,了解数列的分类,理解数列是一种特殊的函数,会用列表法和图象法表示数列;(2)理解数列通项公式的概念,会根据通项公式写出数列数列的前几项,会根据简单数列的前几项写出数列的通项公式.教学重点,难点(1)理解数列是一种特殊的函数;(2)会根据简单数列的前几项写出数列的通项公式.教学过程一.问题情境1.情境:某剧场座位数依次为,,,,,...(1) 某彗星出现的年份依次为,,,,,...(2) 某种细胞,如果每个细胞每分钟分裂为个,那么每过 分钟, 个细胞分裂的个数依次为 ,,,,,...(3) "一尺之棰,日取其半,万世不竭"如果将"一尺之棰"视为 份,那么每日剩下的部分依次为 ,,,,,...(4) 某种树木第 年长出幼枝,第年幼枝长成粗干,第年粗干可生出幼枝,那么按照这个规律各年树木的枝干数依次为 , ,,,,,...(5) 从年到年,我国共参加了次奥运会,各次参赛获得的金牌总数依次为,,,,,.(6)2.问题:这些数字能否调换顺序?顺序变了之后所表达的意思变化了吗?二.学生活动思考问题,并理解顺序变化后对这列数字的影响.三.建构数学1.数列按照一定次序排列的一列数称为数列.数列的一般形式可以写成,,,...,,...,简记为.2.项数列中的每个数都叫做这个数列的项.称为数列的第 项(或称为首项),称为第项,...,称为第项.说明:数列的概念和记号与集合概念和记号的区别:(1)数列中的项是有序的,而集合中的项是无序的;(2)数列中的项可以重复,而集合中的元素不能重复.3.有穷数列与无穷数列项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列.4.数列是特殊的函数在数列中,对于每一个正整数(或),都有一个数与之对应,因此,数列可以看成以正整数集(或它的有限子集)为定义域的函数,当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.反过来,对于函数如果()有意义,那么我们可以得到一个数列,,,...,,....(强调有序性)说明:数列的图象是一些离散的点5.通项公式一般地,如果数列的第项与序号之间的关系可以用一个公式来表示.那么这个公式叫做这个数列的通项公式.四.数学运用1.例题:例 1.已知数列的第项为,写出这个数列的首项、第项和第项.解:首项为;第项为;第项为.例 2.已知数列的通项公式,写出这个数列的前项,并作出它的图象...