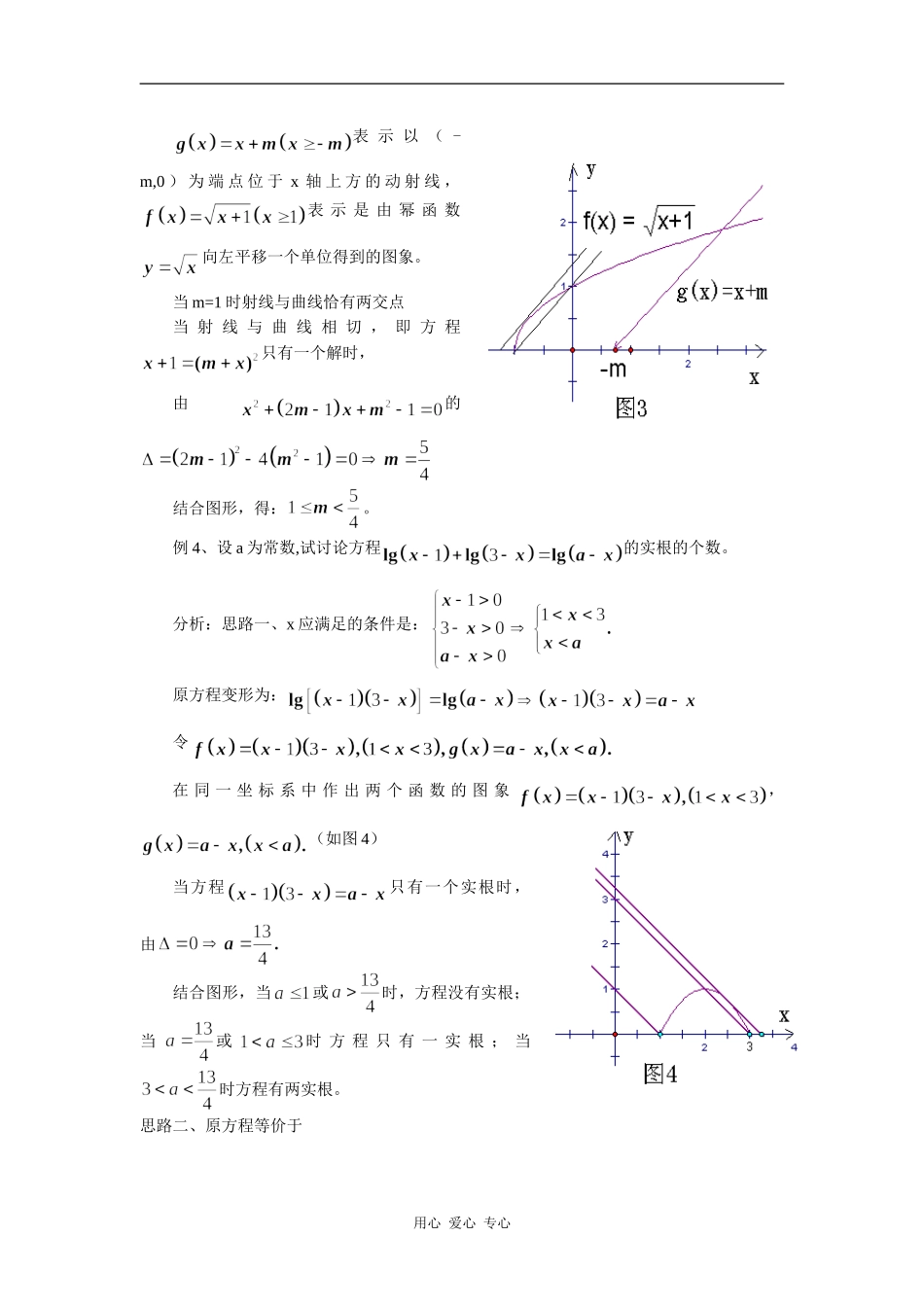
以形示数、数形结合湖南省南县一中 陈敬波(413200)(联系电话号码:13170372039;E-mail:hnnxyzjks@yahoo.com.cn)一普通高中新课标数学教材 A 版必修①的第 86 页介绍方程的根与函数的零点知识,有如下结论:结 论 : 方 程有 实 数 根函 数的 图 象 与轴 有 交 点函 数有零点;并由此很容易得到如下推论:推论:方程有实数根函数的图象与函数有交点函数有零点;二高一学生已经学习了正比例函数、反比例函数、一次函数、二次函数、指数函数、对数函数与幂函数,其中还总结了函数图象的对称与平移知识,于是高一学生有作较丰富多样函数图象的能力。因此我们有必要让学生发挥函数图象的作用,以形示数,数形结合,解决有关方程根的个数问题与含参方程的参数的取值问题及其他应用函数的应用问题。例 1、方程的根的个数是( )A 0 B 1 C 2 D 3分析:思路一、构造函数则∴在内有零点,又在(0,+∞)上为增函数∴在定义域(0,+∞)内仅有一个零点。思路二、令在 同 一 坐 标 系 中 作 出 两 个 函 数与的图象(如图 1)由图可知两曲线只有一个公共点,故方程只用心 爱心 专心有一个解。注 : 在 思 路 一 中 既 要 弄 出, 还 要 说 明在定义域内是单调的,方可得出方程仅有一根。至于函数在整个定义域内不单调,或者不能确定函数的单调性,只能分开讨论解答(见下面的例题 2)。思路二中,只要作出两个函数的图象即可。例 2、判断方程的根的个数分析:思路一、构造函数,函数在定义域内不单调。时,递增,∴在(1,+∞)上有唯一的一个零点。时,恒成立,在上无零点。∴在(0,+∞)上,有且仅有一个零点。即方程的解只有一个。思路二、令:在同一坐标系中作出二者的图象(如图 2)。由图可知方程只有一个解。注:通过两个实例,发现思路二较思路一要简捷些,思路二可以导出思路一中根所在的区间端点,对于方程中含有参数时,思路一无能为力了,请看下面的例题。例 3、若关于 x 的方程有两个不同的实根,求实数 m 的取值范围。分析:将方程变形,引入两个函数,在现一坐标系中作出与的图象(如图 3)。用心 爱心 专心表 示 以 ( -m,0 ) 为 端 点 位 于 x 轴 上 方 的 动 射 线 ,表 示 是 由 幂 函 数向左平移一个单位得到的图象。当 m=1 时射线与曲线恰有两交点当 射 线 与 曲 线 相 切 , 即 方 程只有一个解时,由的结合图形,...