高中数学余弦定理导学案生机勃勃苏教版必修5

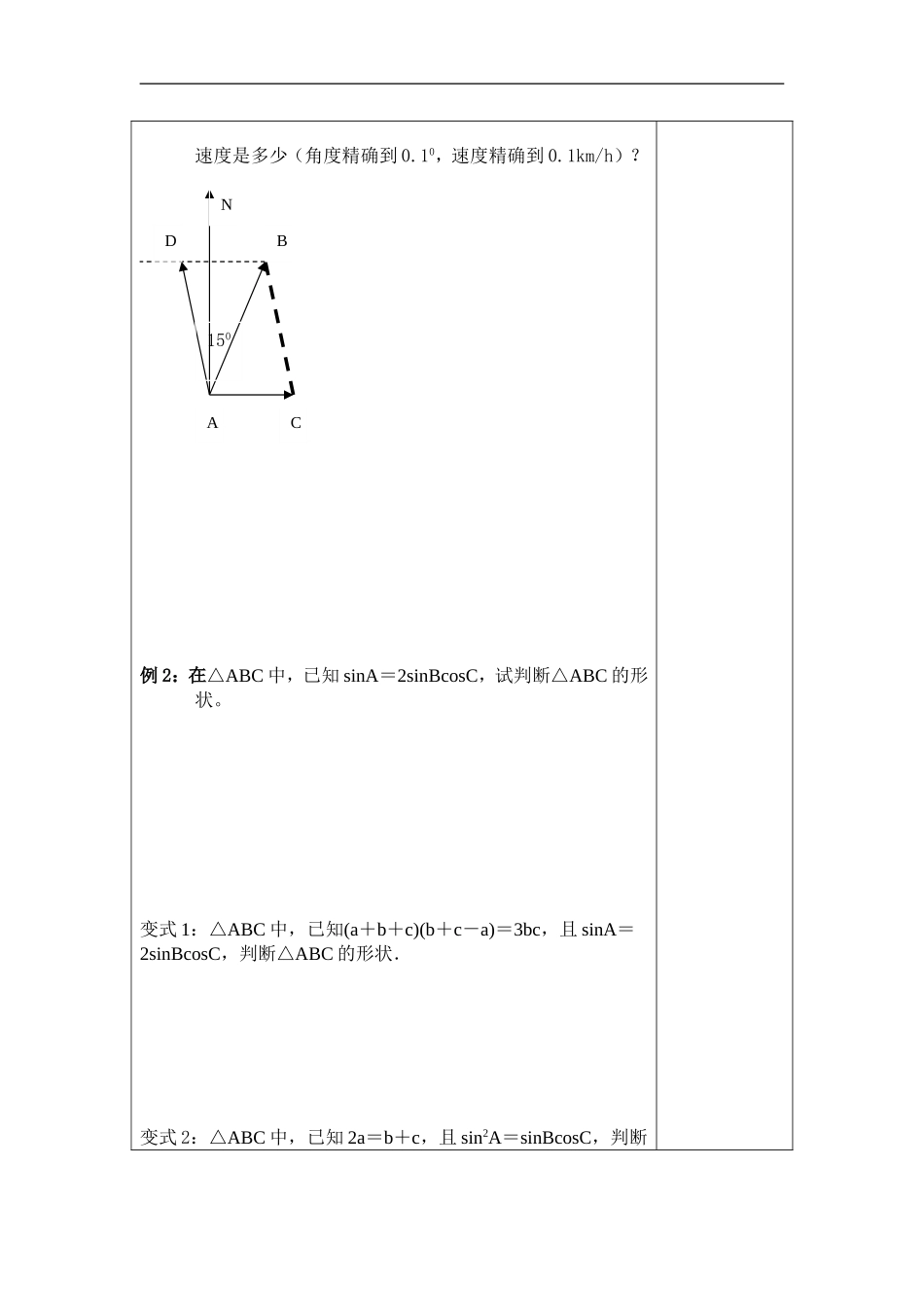
高一数学导学案模板学习内容余弦定理（2）学习目标知识与能力：能够利用正、余弦定理判断三角形的形状；过程与方法：能够利用正、余弦定理证明三角形中的三角恒等式情感态度与价值观：培养学生数形结合的能力学习重、难点重点：余弦定理的应用难点：余弦定理的应用学法指导自主学习，合作交流，探究新知，小组式学习知识链接余弦定理的应用学习过程用案人自我创新一．复习回顾：余弦定理： 小练习：在△ABC 中，（1）已知1800,13,24Cba，求 c , B （2）已知420,10,2Acb，求 a ,B ,C (3 ) 已知13,34,7cba，求最小内角二．例题解析例 1：在长江某渡口处，江水以 5km/h 的速度向东流，一渡船在江南岸的 A 码头出发，预定要在 0.1h 后到达江北岸 B 码头。设 AN 为正北方向，已知 B 码头在 A 码头的北偏东150，并与 A 码头相距 1.2km，该渡船应按什么方向航行？速度是多少（角度精确到 0.10，速度精确到 0.1km/h）？例 2：在△ABC 中，已知 sinA＝2sinBcosC，试判断△ABC 的形状。变式 1：△ABC 中，已知(a＋b＋c)(b＋c－a)＝3bc，且 sinA＝2sinBcosC，判断△ABC 的形状．变式 2：△ABC 中，已知 2a＝b＋c，且 sin2A＝sinBcosC，判断NBDAC150△ABC 的形状例 3：（余弦定理在几何中的应用）AM 是△ABC 的中线，求证：222)(221BCACABAM变式 3：用余弦定理证明：平行四边形的对角线的平方和等于四边的平方和。（方法的多样性）DABC达标检测1.在△ABC 中，如果 sinA : sinB : sinC=2 : 3 : 4,那么 cosC 等于（ ）A. 32 B. 32 C. 31 D. 412.如图，长 7m 的梯子 BC 靠在斜壁上，梯脚与壁基相距 1.5m，梯顶在沿着壁向上 6m 的地方，求壁面和地面所成的角 （精确到 0.10）3. 在△ABC 中，已知 a=2,b=3,C=600,试证明此三角形为锐角三角形.4. 在△ABC 中，设bACaCB ,，且3,3,2baba，求 AB的长（精确到 0.01）BC A学习反思布置作业P17 页 第 5，6 两题